1 뉴론의 구조
신경계 혹은 신경망은 기본적인 단위 구조를 가진다. 즉 이러한 뉴론들이 직병렬로 연결되어 복잡한 네트워크를 구성하게 된다. 아래 그림은 수상돌기의 시냅스를 통해 입력되는 신호의 자중치 부여를 통해 얻어지는 출력 결과가 활성화(activation) 수준의 문턱 전압을 넘는지 못넘는지 이진적으로 처리 후 축색돌기를 통하여 다음 뉴론에 전달하게 된다. 이때 뉴론에서 학습된 가중치값들을 기억하고 있으면 그 다음 입력에 대해서 생리적으로 대응이 가능해지게 된다.

부분의 수상돌기는 앞 단계에 위치한 뉴론으로부터 전기 신호의 입력이 일어나는 부분이다. 이 입력은 시냅스 인터페이스에 의해 뉴론의 핵에서 생화학적인 메카니즘 기반으로 가중(weighting) 처리되어 연산 되고 그 결과 생성된 전압이 문턱값(threshold) 값을 넘기는지 여부에 따라 출력이 결정되며, 이 신경 신호의 전달은 축색돌기 내외부의 이온 농도차 분포 변동을 통해 전달된다.

이와 같은 뉴런 구조에 관해서느 이미 Rosenblatt 이전의 선구자라고 볼 수 있는 McCulloch(신경학자)과Pitts(논리학자)의 1943년 논문에서 잘 들어나 있다. 하지만 Rosenblatt 의 퍼셉트론에 이르러서는 이 뉴론 구조가 학습이 가능하다는 사실을 입증하였다.
참조: McCulloch 과 Pitts, Rosenblatt, Minsky에 이르는 초창기 신경망 ...
http://ejleep1.tistory.com/1407
2 신경망 구성 및 작동 퍼셉트론 사례
머신러닝 인공지능의 초기형태는 1957년 Frank Roselblatt 교수가 발명한 퍼셉트론에 기원한다. 이 시스템은 이미지 데이터를 입력할 수 있는 하드웨어 뿐만 아니라 이를 학습할 수 있는 알고리듬을 포함하여 신경망의 특성을 고스란히 보여 줄 수 있었다.
참조: 머신러닝 퍼셉트론의 선구자 Rosenblatt 전기
http://ejleep1.tistory.com/1061
뉴론의 메카니즘은 생화학적 차원에서 결국 전기 신호가 전달되는 구조이기 때문에 전기, 전자 및 제어분야에서 흔히 사용하는 일종의 블록다이아그램 형태로 신경망(neural network) 모델이 구성되었다.
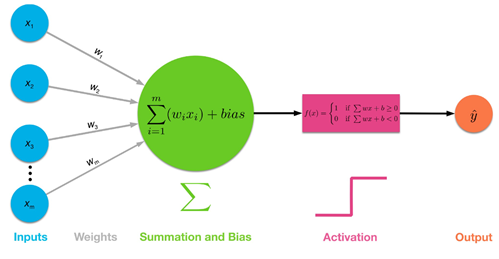
생체 외부로부터의 입력(Inputs)은 피부압박에 의한 압력이라든지 또는 뜨겁거나 차가운 온도와 같은 감각적인 것들과 아울러 시각세포로 이루어진 망막에 맺히는 이미지를 들 수 있는데 이들은 분명히 학습될 수 있다는 점을 우리는 알고 있다. 하나의 뉴론에서 입력의 개수는 하나 또는 그 이상이 될 수도 있다.
가중치(Weights) 부여 과정은 생화학적으로 대단히 복잡한 과정이지만 생확하 반응의 결과인 생체 전압 변화를 추적해 보면 쉽게 이해할 수가 있다. 어느 뉴론이든 자체적인 전압 레벨이 있을 수 있으므로 이 bias 항은 뉴론이 가지는 일종의 DC 오프셋 전압 정도로 이해하면 좋을 듯하다.
뉴론에 전달된 입력값의 가중치와 bias 의 선형적 합산 결과는 반드시 문턱값을 테스트를 거쳐야 한다. 이는 실무율로 알려져 있다. 우리가 어던 느낌을 받으려면 자극(stimuli) 즉 입력 값이 문턱 값을 넘어야 한다는 점이며 문턱값을 넘었다고 해서 그 값을 사용하는 것이 아니라 문터값을 넘었다 아니면 못넘었다는 논리적 사실만 사용한다는 점에 유의하고 이를 이진분류(binary classification) 이라고 한다. 따라서 이 특성으로 인해 뉴론들이 여러개 직렬되어도 전압 상승이 그다지 클 필요가 없다는 점이다.
퍼셉트론 신경망의 학습은 정답에 해당하는 라벨값(label, target)이 알려져 있을때 매번 업데이트를 통해 계속 가중치값을 바꾸어 가면서 테스트하여 적절한 가중치값을 찾아내야 한다. 따라서 퍼셉트론 네트워크 가중치 계산 출력과 이미 알려진 라벨값과의 오차를 계산하여 제어 루프에서의 이득 대신에 적절한 학습률(learning rate)을 곱하여 업데이트 후 재입력하여 새로운 guess 값을 계산해보고 label 값과 비교해 보는 것이다. dl 업데이트 과정은 feedback 제어 과정과 유사한 면이 있는 듯하다. Rosenblatt 교수는 이러한 간단한 알고리듬으로 학습을 시켰으며, 예를 들면 오른쪽 과 왼쪽, 개 아니면 고양이를 식별할 수 있었다.
참조: Rosenblatt N=2 Perceptron Weight Update 알고리듬 Processing 코딩http://ejleep1.tistory.com/1408
3 퍼셉트론 가중치 업데이트
Perceptron 에서는 뉴론에서 입력 데이터에 random 한 초기 가중치를 부여 후 합산하여 다음 예측값(prediction 또는 guess)을 계산하고 그 절대값이 “0” 보다 크면 “1” 또는 “0” 보다 작으면 “-1”인지 여부를 판단하였으며 라벨값과 오차가 발생하는 경우 적절한 이득(gain 또는 learning rate) 값을 곱해 지난번 가중치를 업데이트하였다. Rosenblatt 의 이 알고리듬에서는 항상 일정한 크기의 값을 피드백하기 때문에 매 계산 스텝에서의 연산속도가 가속되지 못하고 일정함을 보이게 된다.

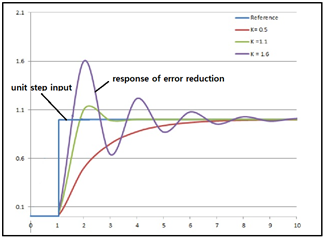
즉 입력 신호가 계단함수(unit step function)처럼 변화할 때 다음 그래프의 PID 제어에서처럼 여러번 진동하면서 결과를 찾아가게 되는데, 이 접근법은 컴퓨팅 연산 효율상 매우 느리므로 Gradient Search 가 머신러닝에서 보편적으로 사용됨에 유의하자.
Rosenblatt 의 단일 계층 퍼셉트론은 AND, OR, XOR 과 같은 로직 문제 해결에도 적용되었다. AND 와 OR 문제는 쉽게 해결이 되었으나 XOR 문제를 해결하지 못한다는 약점이 MIT 의 Minsky 교수에 의해 지적되었다. 이 XOR 문제는 비선형문제이기 때문에 레이어를 하나만 사용해서 해결할 수 없다는 점이 멀티레이어 신경망 발전과 아울러 밝혀졌다.
4. Cost 함수에 의한 퍼셉트론 알고리듬 개선
알려진 label 값과 업데이트된 가중치를 사용하여 계산된 guess 값과의 차이 즉 오차를 줄이는 학습 알고리듬의 비효율성을 제거하기 위해서 가중치들의 연속함수인 Cost 함수를 도입하여 사용하도록 해보자.
아래 식은 k번째 업데이크 과정에서 guess 값과 label값과의 오차를 나타낸다.

이 Cost 함수는 가중치들에 대한 연속함수로 볼 수 있으므로 이 Cost 함수의 최소값을 찾아내기 위해서 미지의 가중치 값에 대한 (편)미분이 가능하다는 점에 유의하자. 아래 그림은 가중치가 하나인 경우의 Cost 함수 사례를 나타낸다.
보다 빠른 연산을 위해 이 Cost 함수의 각 가중치들에 대한 (편)미분 기울기를 계산하여 적절한 이득값 즉 학습률(learning rate)을 곱해 가중치로부터 뺄셈하여 업데이트 하도록 하자. 이는 Gradient Descent 알고리듬에 해당하며 상당히 빠른 연산 속도로 Cost 함수를 최소화 하게 된다. 즉 빠르게 수렴하는 결과를 얻을 수 있다.
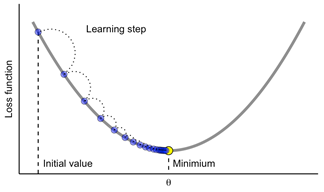
Cost 함수의 특징은 가중치 공간 좌표계에서 최소값을 가지는 아래로 오목한(convex) 한 형상을 가지기 때문에 Gradient Descent 기법을 사용하여 빠르게 가중치를 업데이트 해 나갈 수 있다.

이와같이 Cost 함수를 이용하는 Adaline(Adaptive Linear Neuron) 알고리듬이 1960년에 스탠포드 대학의 버나드 위드로 교수에 의해 제안되었다.
Cross Entropy Cost 함수에 대해서 살펴보자.
Shannon의 엔트로피로부터 유도된 Cross Entropy Cost 함수도 널리 사용된다. Cross Entropy Cost 함수를 도입하기 위해 우선 Shannon의 엔트로피 정의를 살펴보자.
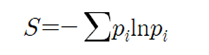
이 공식은 볼트만 엔트로피와 비레상수를 제외하면 수학적 형태는 같으나 물리적 해석이 크게 다르다. 볼트만의 통계역학 관점에서 엔트로피는 최대화되어야 할 물리량이지만 머신러닝에서는 최소화되야 할 Cost 함수에 해당한다.
한편 이 공식은 로그 확률 –ln pi 에 대한 확률적 기대치 표현으로 볼 수 있다.
확률 pi 가 0.0 으로 가게 되면 -ln pi 값이 +∞가 되고 확률 pi 가 1 에 접근하면 값이 0 이 되는 아래 그래프와 같은 특성을 보여준다.

아울러 확률 pi 가 0.0 으로 가도 0.0∙(+∞) 되는 부분은 L’Hospital의 미분 공식에 의해서 0.0 이 됨을 알 수 있다. 학습을 통해서 확률 pi 가 우리가 정답 라벨 값을 알고 있는 one hot code 형태의 클라스 라벨 데이터 값 Yi 에 근접하게 된다.
Cross Entropy Cost 함수를 정의하자.
Cross Entropy ≡ - y_ ⊗ ln p
y_ 는 One Hot Code 로 표현된 컬럼 형태 라벨 값
p 는 class 수에 해당하는 만큼의 컬럼 형 확률 분포로서 그 합은 1.0 이다.
⊗ 는 아마디르 곱 연산을 뜻한다.

따라서 Cross Entropy 는 Shannon 의 엔트로피 공식에서 로그 앞부분을 One Hot Code 로 나타낸 클라스 라벨값으로 대치시킨 결과에 해당한다.
MNIST 예제를 고려해보면 학습을 위한 셈플수가 50,000 개이며 class 수는 10 이다. 만약 mini-batch 크기를 100 개 단위로 한다면 총 mini-batch 수 B 는 5,000 개가 된다.
Binary classification을 고려하자. 이때 확률 함수 p는 Sigmoid 함수를 사용할 수 있다, 아울러 binary 일 경우 softmax 함수는 결국 Sigmoid 함수가 됨에 유의하자.

위 식을 사용해 Cross Entropy 를 작도해 보자. log 값 계산 시 0.0 입력이 불가능 하므로 극한값 개념에서처럼 아주 작은 값 0.01 정도의 작은 값을 넣도록 한다.
아래의 작도 결과를 관찰해 보면 Cross Entropy 는 최소값을 가지는 Cost 함수가 될 수 있음을 알 수 있다.
| import numpy as np import matplotlib.pyplot as plt p =np.linspace(0.0, 1.0, 100) s = -np.log(p)-np.log(1-p) plt.plot(p,s) |

분류 클라스가 3 인 아래의 경우들을 살펴보자.

Keras 에서 TensorFlow==2.92 버전을 사용해 MNIST 머신러닝 코드를 실행해 보자.
구글 Colab 에서 TensorFlow==2.92 버전을 사용한 MNIST 예제 코드
loss-fn = ... 라인을 skip 하고 실행해 보자.
https://ejleep1.tistory.com/1441
한편 TensorFlow==1.15 버전 MNIST 코드와의 차이점을 살펴보자.
구글 Colab 에서 TensorFlow==1.15 버전을 사용한 MNIST 예제 코드
https://ejleep1.tistory.com/1440
Keras 에서는 사용자가 임의로 loss 함수를 작성하는 것이 아니고 지정된 loss 함수를 사용하도록 한다.
Keras Loss Functions: Everything You Need To Know
'인공지능 응용 공학' 카테고리의 다른 글
| Wine 데이터와 PCA(Principal Component Analysis) 처리 (0) | 2022.11.02 |
|---|---|
| 인위적으로 생성한 2그룹 데이터를 이용한 퍼셉트론 예제 (0) | 2022.10.30 |
| Iris flower data를 이용한 Rosenblatt 퍼셉트론 파이선 코딩 (3) | 2022.10.29 |
| Rosenblatt N = 2 Perceptron Weight Update 알고리듬 Processing 코딩 (0) | 2022.10.27 |
| McCulloch과 Pitts, Rosenblatt, Minsky에 이르는 초창기 신경망 연구의 역사 명과 암 (0) | 2022.10.27 |