
2차원 평면상에서 타원 내부에 위치하고 있는 2차원 데이터들을 관찰해 보자. 이 데이터들은 서로 수직하는 장축과 단축으로 이루어지는 타원 영역 내에 위치하고 있다. 이와 같이 분포하고 있는 데이터들의 분산 값이 최대가 될 수 있는 축들을 주축(Principal Axes)이라 하며 위의 2차원 분포에서는 2개의 서로 수직한 주축을 찾아낼 수 있는데 하나는 장축이 되며 다른 하나는 단축이 된다.
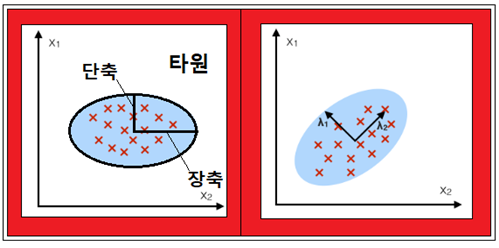
통계학적 측면에서 타원의 주축들은 분산 값에 대응한다. 즉 데이터들의 평균이 얻어지면 (데이타-평균)의 제곱 값을 합산하여 분산 값이 최대가 될 수 있는 두 개의 축을 찾을 수 있다. 이런 경우에 (데이타-평균) 값들로 매트릭스를 형성하여 그 Transpose 와 곱하였을 때 대각선 성분들만 남는다면 데이터들은 서로 직교(orthonormal)하면서 상관관계가 없는 uncorelated된 주성분들(Principal Components)이 된다.

즉 PCA(Principal Component Analysis)기법은 서로 상관성이 있는 데이터들(corelated data)을 직교변환(orthonoral transform)시켜 선형적으로 상관관계가 없는 주성분들(Principal Components)을 얻어내는 기법이다.
LDA기법에서도 변환 W가 있으며 아래와 같이 J(W)를 최대화 하는 반면에 PCA에서는 Variance를 최대화하는 주축들을 찾는 과정으로서 Variance 로부터 구성되는 매트릭스의 eigenvalue 문제 로 귀착된다.
붓꽃 데이터만 해도 4개의 특징들로 구성되는 차원(Dimension)이 4인 데이터이다. 차원이 4인 이 데이터를 시각적으로 작도할 수는 없지만 자연에서 채취한 랜덤한 데이터로서 서로 상관성이 있는 데이타라 볼 수 있을 것이다. 차원이 4인 상태에서 Varaince 값을 최대화 할 수 있도록 좌표 변환을 해보면 4개까지의 주축을 찾을 수도 있을 것이다.
한편 PCA에 의해 찾아지는 방향들은 데이타 스케일링에 아주 민감하므로 표준화 처리를 하는 것이 좋다.
표준화된 데이터를 사용하여 Covariance 계산하여 매트릭스를 구성한다.
Covariance 매트릭스를 사용하여 eigenvalue 방정식을 구성하고 eigenvalue를 계산한다.
eigenvalue 가 크기 순으로 얻어지면 큰 값 순으로 eigenvector를 계산하여 PCA 방향을 결정한다.
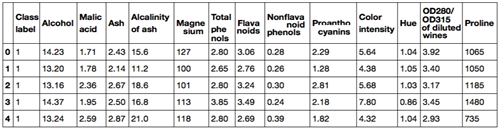
PCA 기법 예제를 코딩하기 위해서 미국의 UCI 대학 서버에서 가져다 쓸수 있는 Wine 데이터를 사용해 보자. 178개의 샘플로 구성된 Wine 데이터 각각은 와인에 포함되어 있는 13가지 화학물질 성분들을 특징(feature) 로 삼는다. 이 와인들은 3개의 class 로 분류되는데 이탈리아의 같은 지역에서 재배되는 3가지 서로 다른 재배종으로부터 유래된 포도 유형을 나타낸다.
이 데이터를 url 주소로부터 읽어 들여 표준화 하자.
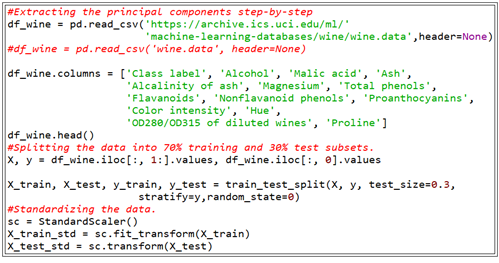
항상 읽어 들이는 데이터가 리스트 형으므로 ∼.values 명령을 사용하여 NumPy 형 어레이 데이터로 변환하여 사용한다.
표준화된 데이터들을 사용하여 Covariance 값을 계산하자. 표준화가 되었으면 샘플들의 특징(feature)별 평균값은 0 이 된다.
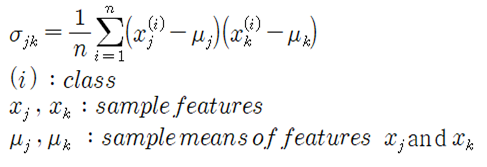
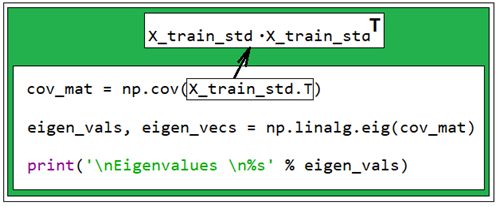
178개의 샘플 데이터들 중 학습용(X_train, X_train_std)으로 사용할 70% 는 124개이다. Covariance 매트릭스는 13X124 매트릭스와 124X13 매트릭스를 곱하면 13X13 매트릭스가 얻어진다.

크기순으로 informative 하다. 즉 중요도가 크다. 이 eigenvalue 로부터 크기가 1.0 인 eigenvector 가 13개 계산된다. 이들 간의 곱은 orthonomal 조건을 만족해야 하므로 거의 0.0 이 되어야 한다. eigenvalue 계산 후 아래의 루틴을 추가해 계산해 보면 서로 다른 eigenvector들 간의 곱은 0.0 이 되면서 자체 크기는 1.0 이 됨을 알 수 있다. 참고로 LDA기법에서도 eigenvector들이 얻어지지만 서로 orthonormal 하지는 않음에 유의하자.

Variance_explained ratio 를 계산해 보자. 이는 계산된 eigenvalue 값들의 전체 합에 대한 개별 eigenvalue 값의 비율이다. 첫 번째와 두 번째 eigenvalue를 합하면 전체의 거의 60%를 차지한다. 아래 그림을 참조하자.
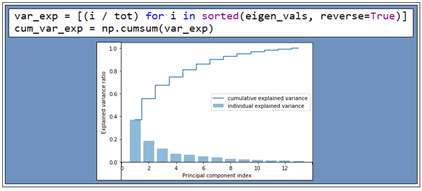
13개의 eigenvaule들이 얻어졌고 각 eigenvalue 별로 eigenvector들이 구해졌다. 그 다음 각 eigenvector들의 첫 번째와 두 번째 성분까지 만을 사용하여 차원을 낮추기 위한 13X2 변환 매트릭스 W를 구성하자.

178개중의 하나인 샘플 데이터X는 1X13 매트릭스로 표현이 된다. X 곱하기 W는 1X13X13X2 즉 1X2 즉 PC1, PC2 평면상에 작도해 볼 수 있는 좌표로 변환된다.
아래와 같이 PC 평면에서 데이터를 작도하고 Logistic Regression을 적용해 보면 Classification 이 잘 되고 있음을 알 수 있다.
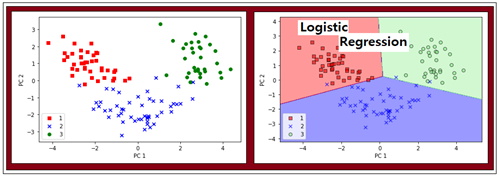

이와 같이 PCA 과정을 훑어보았다. 과연 이 PCA 정식화는 누구로부터 시작되었는가? 좀 아득한 옛날 Fisher 교수 이전 세대로서 통계학의 기초를 닦았던 Pearson 이라고 통계학에서 너무나 유명한 분이 있는데 PCA기법은 물리학이나 탄성학(재료역학)에서 다루는 응력의 주축해석법의 아날로지로서 Pearson에 의해 1901년에 발명되었다. 아울러 The Grammar of Science 라는 Pearson 의 유명한 저서는 상대성 이론의 토대를 제공할만한 주제들을 이미 다루어 20년가량 연배가 아래인 아인슈타인이 읽고 상대성 이론 연구에 영향을 미쳤다고 한다.
#PCA_01.py
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from matplotlib.colors import ListedColormap
from sklearn.linear_model import LogisticRegression
#Extracting the principal components step-by-step
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/'
'machine-learning-databases/wine/wine.data',header=None)
#df_wine = pd.read_csv('wine.data', header=None)
df_wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash',
'Alcalinity of ash', 'Magnesium', 'Total phenols',
'Flavanoids', 'Nonflavanoid phenols', 'Proanthocyanins',
'Color intensity', 'Hue',
'OD280/OD315 of diluted wines', 'Proline']
df_wine.head()
#Splitting the data into 70% training and 30% test subsets.
X, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
stratify=y,random_state=0)
#Standardizing the data.
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
cov_mat = np.cov(X_train_std.T)
eigen_vals, eigen_vecs = np.linalg.eig(cov_mat)
print('\nEigenvalues \n%s' % eigen_vals)
print('\nEigenvalues \n%s' %eigen_vecs)
cross_sum = 0.0
self_sum = 0.0
for i in range (13):
cross_sum = cross_sum + eigen_vecs[1,i]eigen_vecs[2,i]
self_sum = self_sum + eigen_vecs[3,i]eigen_vecs[3,i]
print(cross_sum)
print(self_sum)
tot = np.sum(eigen_vals)
print(tot)
var_exp = [(i / tot) for i in sorted(eigen_vals, reverse=True)]
cum_var_exp = np.cumsum(var_exp)
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center',
label='individual explained variance')
plt.step(range(1, 14), cum_var_exp, where='mid',
label='cumulative explained variance')
plt.ylabel('Explained variance ratio')
plt.xlabel('Principal component index')
plt.legend(loc='best')
plt.tight_layout()
plt.show()
#Make a list of (eigenvalue, eigenvector) tuples
eigen_pairs = [(np.abs(eigen_vals[i]), eigen_vecs[:, i])
for i in range(len(eigen_vals))]
#Sort the (eigenvalue, eigenvector) tuples from high to low
eigen_pairs.sort(key=lambda k: k[0], reverse=True)
w = np.hstack((eigen_pairs[0][1][:, np.newaxis],
eigen_pairs[1][1][:, np.newaxis]))
print('Matrix W:\n', w)
#Trnasformed wine data plot on PC plane
X_train_std[0].dot(w)
X_train_pca = X_train_std.dot(w)
colors = ['r', 'b', 'g']
markers = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), colors, markers):
plt.scatter(X_train_pca[y_train == l, 0],
X_train_pca[y_train == l, 1],
c=c, label=l, marker=m)
plt.xlabel('PC 1')
plt.ylabel('PC 2')
plt.legend(loc='lower left')
plt.tight_layout()
plt.show()
'인공지능 응용 공학' 카테고리의 다른 글
| TensorFlow solution of x - 1.12345 = 0 (0) | 2022.11.05 |
|---|---|
| 신경망(Neural Network) 연구의 역사 (0) | 2022.11.02 |
| 인위적으로 생성한 2그룹 데이터를 이용한 퍼셉트론 예제 (0) | 2022.10.30 |
| 뉴론의 구조와 퍼셉트론, Shannon의 엔트로피, Cross Entropy? (0) | 2022.10.30 |
| Iris flower data를 이용한 Rosenblatt 퍼셉트론 파이선 코딩 (3) | 2022.10.29 |