
열역학(Thermodynamics)에서 Thermo 란 열을 뜻하며 dynamics는 변동을 뜻한다. 즉 열역학이란 시스템의 열적 변화를 따져보는 것이 된다.
열역학적 Control Volume 이 잘 정의된 시스템의 경계를 통해 열출입 ∆Q 가 일어나게 되면 아울러 내부의 압력 변동에 따라 Control Volume 의 변동에 따라 일(Work) ∆W 가 행해진다.
특히 Control Volume 경게를 통한 열출입 ∆Q=0 이면서 일 ∆W=0 인 이상기체의 물리적 상태를 고려해보기로 한다.
1800년대 후반에 볼츠만은 미시적인 원자나 분자의 물성이 물질의 거시적인 상태에서의 물성과 어떤 관계에 있는지를 깊이 고찰하여 물리학에서 통계역학의 토대를 쌓았으며 그의 대표적인 아이디어가 바로 볼츠만 분포와 엔트로피 공식(S=k lnW)일 것이다. (※ 볼츠만 엔트로피 공식에서의 W 는 일이 아닌 에너지 수준별 기체분자 운동의 경우의 수를 뜻한다.)
볼츠만의 연구내용을 요약해 보면 용기 속에 가두어둔 수많은 개개의 기체 입자들의 미시적인 관점에서 위치와 에너지를 고려하여 거시적인 관점의 열역학적 상태 변수 압력, 부피, 온도, 엔트로피와의 관계를 설정하는 작업이었다.
위 그림에서처럼 입자 또는 기체가 처해 있는 상태를 보여주는 열역학 시스템은 1 법칙과 2 법칙을 만족한다. 열역학 1 법칙은 열역학 시스템에 외부로부터 열이 가해지거나 또는 외부로부터 시스템 용기에 힘을 가해 용기의 부피가 감소하도록 일(Work)을 해주게 되면 시스템 내부의 물질인 기체의 내부에너지가 증가하게 된다는 것이다. 내부에너지 증가는 결국 용기 내부의 압력과 온도 증가로 이어질 것이다.
따라서 현재 고려하는 그림 상의 용기 시스템은 단열상태에서 외부에서 용기를 압축할 정도의 외력 작용이 없으므로 용기 내부 기체는 일정한 온도를 유지할 수 있을 것이다. 이러한 논의는 기체 입자로 채워진 용기 시스템의 거시적 상태 중 온도(T)를 기술하는 것이며 마찬가지로 압력(P), 부피(V), 엔트로피(S)도 거시적 상태 변수에 포함된다.
볼츠만 분포 문제를 다루기 위해 용기 내 입자들에 대해서 몇 가지 가정을 설정하자. 그 설정에 따라서 볼츠만 확률분포 공식이 유도되는 것이며 한편 머신러닝 이미지 처리 분야에서 이 볼츠만 분포를 차용하려면 도입하는 가정들도 적합해야 할 필요가 있다.
충돌이 일어나 서로 에너지를 교환할 수 있는 동일한(identical) 종류의 입자들의 운동을 고려한다. 입자가 동일하다는 것은 물리적 측면에서 물성이 같다는 것이며 한편으로는 이 입자와 저 입자를 서로 구분할 수(distinguishable) 있다고 가정한다. 왜냐면 입자들이 같은 속도를 가진 경우에 운동 에너지는 같을지 몰라도 적어도 운동 방향을 나타내 주는 벡터인 운동량 값이 같을 수는 없으며 아울러 입자의 위치도 달라 이들을 서로 구분할 수 있다는 점이다.
특히 동일한 입자들을 고려하려면 쉽게 말해서 용기 속에 같은 종류의 기체 물질 즉 순수한 산소라든지 또는 순수한 질소라든지 한 가지 물질을 넣어두는 상황으로 이해하면 좋을 듯하다. 공기의 경우 산소와 질소가 일정 비율로 혼합되어 있지만 혼합된 비율의 덩어리를 하나의 이상기체 입자로 보면 될듯하다.
입자의 종류로는 분자, 먼지, 돌맹이, 곡식 낱알 등을 포함할 수 있는데 소립자 같이 현대 물리학에서 다루는 대상들은 서로 구분이 안 되는(indistinguishable) 경우가 많으므로 배제하도록 한다.
절연이 잘된 상태의 고립된(isolated system) 용기(상자)에 포함된 이 입자들은 서로 충돌하게 되면 에너지를 교환할 수 있으며 열적으로 평형(thermal equilibrium)을 이루고 있음과 아울러 이 입자들의 총 에너지의 합이 일정하게 유지된다고 가정하자. 에너지 교환이 일어나는 입자들의 충돌이 탄성 충돌이라면 비탄성 충돌에서처럼 마찰이나 열 변환에 따른 손실이 없어 에너지가 보존된다.
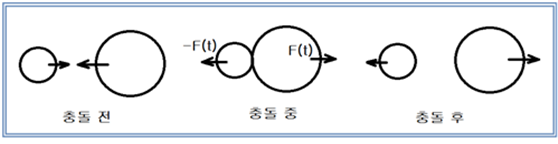
단열이 잘된 상태의 고립된(isolated system) 용기(상자)에 포함된 이 입자들이 기체 상태로 들어 있다고 가정하자. 단열이 잘되어 있으므로 시간이 경과해도 온도를 측정해 보면 일정 온도를 유지할 것이다. 상자 내부에서는 동일한 입자들이 각각 서로 다른 운동 에너지를 가지고 운동하면서 많은 충돌이 일어나고 있을 것이다. 용기 내부의 입자들의 전체 에너지는 외부와의 절연으로 인해 빠져 나가는 열에너지 없이 일정한 상태로 계속 유지되어야 하며 또한 입자들의 충돌에 있어서 충돌 전후에 에너지가 보존되려면 탄성충돌이라야 한다.
이러한 입자들이 포함된 용기의 내부 온도가 일정하고 입자들의 전체 에너지가 보존된다는 조건 아래에서 각각의 입자들은 서로 다른 위치와 속도분포에 따라 물리적으로 가능한(probable) microstate의 경우의 수가 수없이 많아지게 되므로 통계적인 확률분포로 기술할 필요성이 제기된다.
따라서 실제로 용기 내부의 기체 압력이 충분히 낮다면 앞서의 가정들이 잘 맞는 이상기체(ideal gas)로 볼 수 있기때문에, 수많은 microstete로 이루어지는 통계적 앙상블에 대해 소수의 거시적 상태 변수 즉 P(압력). V(부피), T(절대온도), S(엔트로피)를 사용하는 열역학의 이상기체 법칙에 의해 거시적인 macrostate를 잘 표현할 수 있다.
한편 흑백 명암의 픽셀로 구성된 가로와 세로가 동일한 크기의 사각형 이미지를 고려해 보자. 픽셀들의 크기는 다 동일하지만 픽셀은 위치 정보와 흑백 명암 정보를 가질 수 있는데 그 값들은 서로 다를 수 있다. 흑백 명암정보는 0∼255 까지의 범위 내에서 정수로 표현이 가능하다. 하지만 볼츠만 분포에서 입자들은 운동이 일어나 위치와 속도가 Random 하게 변화되지만 픽셀은 운동을 할 수 없기 때문에 운동에너지 개념을 도입할 수는 없는 대신에 명암을 나타낼 수 있도록 0∼255 까지의 범위를 가지는 데이터로 설정하고 픽셀 별로 특정한 가중치와 편향을 도입하여 확률적으로 다룰 수 있는 outcome 화가 가능해진다. 우리가 다루는 이미지 수기문자의 범위가 0~9 까지의 10가지라면 각 숫자 이미지별로 얻어지는 샘플들의 평균 outcome 들에 대해서 하나의 확률이 정의될 수 있으며 이들 전체의 합은 1.0 이 되어야 할 것이다.
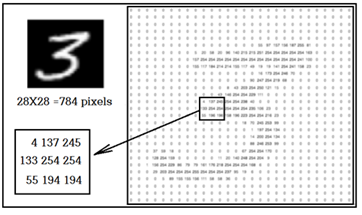
위 흑백 이미지는 수기로 쓴“3”자 MNIST 데이터의 하나이다. 이미지를 표현하고 있는 픽셀 정보를 살펴보면 0∼255 사이의 정수값을 가짐을 알 수 있다. 이러한 샘플들을 각 숫자별로10개씩 도합 100개의 batch 샘플을 대상으로 앞서 언급한 것처럼 가중치와 편향을 사용하여outcome 화가 가능할 것이다.
MNIST머신 러닝 코드를 실행하게 되면 한 번의 batch 실행에 6만개의 데이터 샘플 중에batch 단위로 데이터들을 샘플하여 학습하는 바 “3”지라 해도 아래와 같이 여러 가지 종류의 이미지가 샘플 될 수 있다. 6만개 중“3”자 이미지가 십분의 일인 6천개가 있을 수 있다.

통계 역학 앙상블에서 용기 속의 입자들이 충돌을 통해 에너지를 교환하게 되지만 그래도 거시적으로 즉 macrostate 즉 압력, 온도, 부피, 엔트로피는 그대로 유지가 된다는 사실을 알고 있다. 이미지에서도 이미지별 픽셀 데이터 값 변동으로 픽셀의 microstate 가 변동되어도 이미지의 거시 정보(macroscopic data)는 그대로 유지 되어야 할 것이다. 즉 위 그림의“3”자 샘플 이미지를 조사해 보아도 그 microstate에 해당하는 세부적인 픽셀의 위치와 값을 조사해보면 다 다를 수밖에 없지만 거시적인 정보로서 이들은 모두 다 ”3“으로 분류(classification) 되는 것이므로 각 이미지별로 outcome 값과 주어진 라벨 값과의 차이의 제곱을 합하여 Cost 함수화 한 다음에 경사하강법과 같은 최소화 기법을 적용해 도입된 가중치와 편향 값 결정이 가능하며 이 과정이 바로 학습 즉 learning에 해당한다.
따라서 통계적 앙상블로서 microstate를 구성하는 상자 속의 입자들이 고전 물리학에서의 볼츠만 확률분포에 의해서 거시적인 macrostate 를 제대로 기술할 수 있다면 이미지를 구성하는 픽셀들도 유사한 확률분포에 의해 이미지의 거시 정보(macroscopic data)를 추출할 수 있는 가능성이 부여된다.
물리학적 관점에서 볼츠만의 결론은 확률적으로 기술이 가능한 microstate의 수에 로그 값을 취하여 일정한 상수즉 볼츠만 상수를 곱하여 엔트로피로 정의한 후 물리학적인 시스템내에서 이 엔트로피가 최대값을 가지는 경우에 물리적 평형 상태가 이루어진다고 한다.
반면에 머신러닝에서도 거의 동일한 공식을 차용하여 엔트로피를 정의하는 바 이는 정보과학에서 엄청난 공적을 남긴 Shannon 교수의 엔트로피로서, 이 엔트로피는 최소화 되어야 함에 유의하자. 이와같이 엔트로피를 최소화하는 머신러닝의 명령이 바로 softmax 이다. 이 내용은 Bishop 교수의 명저 "Pattern Recognition" 에서 Shanon 교수와 컴퓨터 및 CPU 구조 발명의 원조인 폰 노이만 박사와의 대화에서 그 근거를 찾아 볼 수 있다. 양자역학 분야에 폰 노이만 박사 자신의 이름이 명명된 엔트로피가 있으나 물리학계에서 하도 논쟁에 시달려 피곤함을 느낀 경험을 바탕으로, Shannon 교수에게 통계역학 어쩌구 저져구 하다가 학계에서 괜히 시달리지 말고 아예 자네 이름으로 특별한 엔트로피를 정의하는 것이 좋겠다고 권고했다는 내용이다.
보다 구체적으로 아래의 블로그에서 Shannon 의 엔트로피를 머신러닝에 맞춰 더욱 구체화한 Cross Entropy 에 대해서 알아보자.
https://ejleep1.tistory.com/1411
뉴론의 구조와 퍼셉트론, Shannon의 엔트로피, Cross Entropy?
1 뉴론의 구조 신경계 혹은 신경망은 기본적인 단위 구조를 가진다. 즉 이러한 뉴론들이 직병렬로 연결되어 복잡한 네트워크를 구성하게 된다. 아래 그림은 수상돌기의 시냅스를 통해 입력되는
ejleep1.tistory.com
'인공지능 응용 공학' 카테고리의 다른 글
| 텐서플로우 선형회귀법 예제 (1) | 2023.01.03 |
|---|---|
| Information Bit Number 및 Entropy 계산 (0) | 2022.11.08 |
| TensorFlow solution of x - 1.12345 = 0 (0) | 2022.11.05 |
| 신경망(Neural Network) 연구의 역사 (0) | 2022.11.02 |
| Wine 데이터와 PCA(Principal Component Analysis) 처리 (0) | 2022.11.02 |