
시작 바에서 Anaconda3(64 bit) 의 Jupyter Notebook(anaconda3)을 클릭하자.
최근 윈도우즈 10 PC에서는 CPU의 부동소숫점 기준 자리수가 64비트 기준으로 상향되었다. 참고로 과거의 윈도우즈 7 XP 에서는 32비트가 표준이었다.
※ 신호처리용 DSP 칩의 경우는 여전히 32비트 수준에 머무르고 있다.
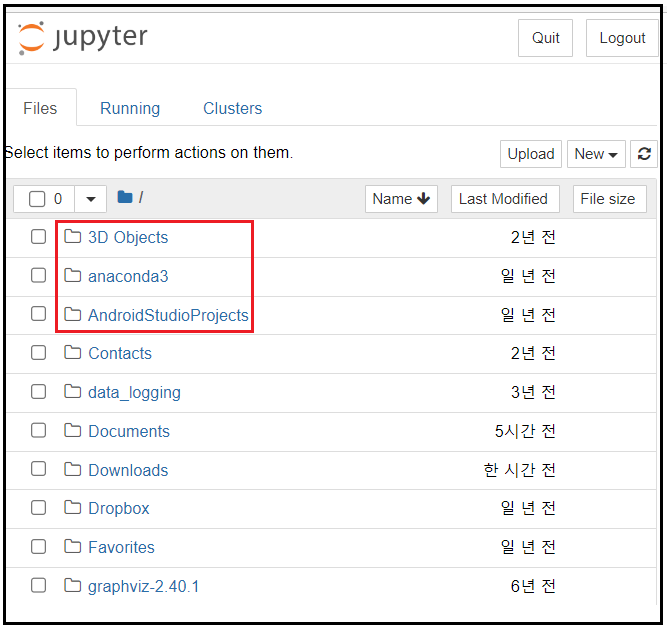
쥬피터를 처음 열었을때의 스크린샷이다.
3D objects, anaconda3, AndroidStudioProjects 폴더들이 있다.
윈도우즈 10 파일 탐색 기준으로 이들의 위치를 확인해보자.
학습문제) 사용자 PC별로 위 폴더들이 어디에 있는지 확인해 보자.
바탕화면의 사용자 폴더를 열어 보자.
PC개인사용자 폴더 안에 3D objects, anaconda3, AndroidStudioProjects 폴더들 확인이 가능하다.
한편 .android를 비롯하여 윈도우즈 PC에 설치한 소프트웨어들 확인이 가능하다.
"." + 소프트웨어 명을 사용하는 이유는 다른 유사한 파일명과 구분하기 위해서이다.

문서 아이콘을 클릭하여 무엇이 들어 있는지 확인해 보자.
아두이노, 인텔의 Openvino, Processing, Visual Studio, 카카오톡 다운파일 폴더들을 확인할 수 있다.

내 PC 파일 탐색 기준에서 보면 개인 사용자 폴더는 C:/사용자 폴더/ 안에 위치하고 있음을 알 수 있다.

한편 시작 바의 아이콘을 사용하여 jupyter notebook 을 열수도 있지만 시작 바의 Anaconda Prompt 창에서 command line 명령인 jupyter notebook 을 타이핑하고 엔터키를 쳐서 열수도 있다.
※ Anaconda Prompt 창에서 (base) C ... 로 시작하는 command line 명령에서 (base) 는 Anaconda3 의 기본 가상환경인 (base) 를 의미한다.

New 버튼을 사용하여 새로이 파일을 열어보자.

사용자 별로 작성한 jupyter notebook 코드를 저장할 수 있도록 개인사용자 폴더->문서->jupyternb 폴더를 미리 준비하고 작성한 코드를 untitled1.ipynb 에서 Mycode.ipynb 로 수정하여 저장해 보자.
서류 및 파이선 코드의 헤딩 작성
Mycode.ipynb에서 일종의 웹 서술 HTML 언어인 Markdown 언어 처리를 살펴보자.
일단 HTML과 유사하게 타이핑하여 서류의 헤딩을 작성 후 Code-->Markdown 을 선택하면 셀에서 웹 처럼 변환된다.
# 갯수에 따라 헤딩 문자 크기를 조절 출력할 수 있다.

expression of equation 에서는 함수 f(x,y)=squareroot(x^2+y^2)을 Code에서 입력하여 Markdown에서 Run Cells 해 보도록 한다. 아울러 적분과 미분공식도 연습해 보자. $\∙∙∙$ 형식에 의한 수학공식 표현은 Microsoft Word 가 출현 하기 전이었으며 당시 Word Perfect 란 워드가 사용되던 1980년대에 파퓰러하게 사용되던 Tex, LaTex 문법이 inline 방식으로 살아남아 그대로 적용되고 있다. $$\∙∙∙$$ 형식은 표현식이 중앙에 자리 잡게 된다. 아주 복잡한 수식 체계를 표현하려면 Tex, LaTex 문법을 참고하여 사용하기 바란다. LaTex 포맷은 80년대 말 IBM XT가 보급되던 시절부터 대학에서 보유했던 메인 프레임 방식의 중형 컴퓨터였던 VAX 시스템에서 흔히 사용되던 워드프로세서였으며 아직도 살아남아 사용이 되는듯하다.

셀 계산: 덧셈, 뺄셈, 곱셈, 나눗셈, 지수계산
※ 삼각함수, 로그함수 계산은 별도의 수학 라이브러리 numpy의 지원이 필요하다.

자료유형 확인: 정수, 실수, 문자

변수 설정 및 출력, 명령 분리 ; 사용

리스트 데이터: 파이선 연산에 대단히 편리한 데이터 구조, 리스트 데이터 순번은 항상 0 부터 시작

리스트 데이터 슬라이싱 용법

원소가 2개인 리스트

딕셔너리: 리스트는 인댁스 번호로 0,1,2,3,... 순서로 데이터 값을 저장하는 반면에 딕셔너리는 key 와 함께 value 를 쌍으로 데이터를 저장하므로 key 를 호출하면 값을 불러온다.

Boolean Data 는 참(True) 과 거짓(False) 형태의 진리 값을 다루는 자료형이다.이 Boolean Data는 AND, OR, NOT, XOR 과 같은 논리 연산자를 사용할 수 있다.

matplotlib.pyplot을 사용하여 그래프를 작성 출력해보자. 리스트 데이터 [1,2,3,4] 는 리스트 데이터형 x 구간 [0.0, 1.0, 2.0, 3.0] 에 y 축 함수 값 [1, 2, 3, 4] 를 의미한다.

함수 작도를 위해서는 가로축 및 세로축 데이터를 리스트 구조로 준비하자.
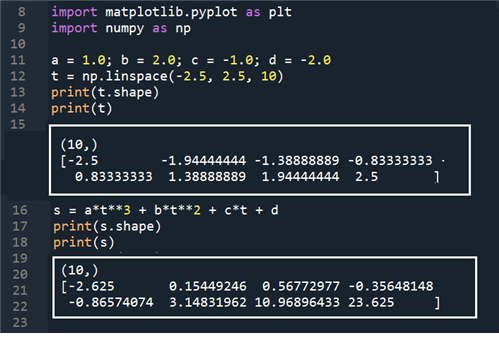
NumPy 명령인 linspace 는 구간 [left, right] 로 표현되는 가로축 구간을 n 개로 이산적인 점들로 정의하여 nparray 리스트 형태로 출력한다.
np.linspace 로 생성한 nparray(리스트데이터) 형태의 구간 t 를 사용하여 함수 s 를 계산하면 s 역시 nparray(리스트데이터) 구조로 얻어진다.
plot 명령에서 가로축 및 세로축 데이터만 사용하면 선형으로 연결된 그래프가 작성된다. 점은 “o” 나 “x”를 사용하고 색상을 추가로 정의해주면 이산적인 작도가 가능하다.

코드에서 사용된 변수 t 와 s 의 shape 을 출력해 보자. 즉 plot 에 사용되는 구간값과 함수값에 nparray(리스트데이터) 구조의 데이터가 사용될 수 있다.
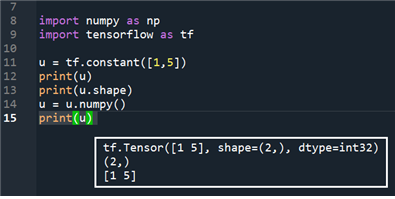
TensorFlow에서 설정된 텐서플로우 상수의 값과 shape 을 출력해 보자. 아울러 텐서플로우 상수를 numpy() 로 변환하여 출력해보자.
첨부된 쥬피터 파일을 다운받아 실습해 보자.
파이선에서 콜론 즉 “:”으로 끝나는 IF 제어문 이후 들여쓰기(Indentation)는 4칸으로 규정되어 있다.
IF 문의 구조는 if, elif,..., else 형태로 사용한다.

FOR 제어문도 IF 제어문처럼 콜론 즉 “:” 으로 끝나고 4칸 들여쓰기를 해야 한다.

※ 기타
⓵ while true 무한루프
⓶ try:
exception: 무한루프
⓷ if ⦁⦁⦁:
⦁⦁⦁
continue( or break)
함수

class 내에 정의된 함수를 메서드(method) 라 하며 인수(argument)를 적용하여 class 밖에서 class를 상속하여 계산한 결과를 instance 라고 한다.

class 구성은 초기화 루틴 즉 def __nit__(self, name) 이 필수적이며 instance 연산 시 오직 한 번만 초기화하면 되며 메인 코드에서 별도로 불러서 상속 시킬 필요가 없다.
반면에 이 예제에서 “hello(self)” 나 “”goodbye(self)“ 의 경우는 일단 instance 연산을 위해 class Man을 불러 상속을 준비해야 하며 여기서는 하단 메인 코드의 ”m = Man(”Tom“)” 이 그 작업에 해당한다.
m.hello() 는 Man(“Tom”).hello()와 동일한 의미이다.
m.goodbye()도 Man(“Tom”).goodbye() 와 동일하다.
일단 class Man을 인수 “Tom”으로 한 번 호출했으므로 그렇게 초기화 된 상태에서 몇 번이고 다시 hello() 나 goodbye()를 사용할 수 있지만 다시 다른 인수 즉 예를 들자면 “Robert” 로 인수를 변경하게 되면 다시 초기화 한후 “Robert”에 대한 class Man(“Robert”)을 호출하여 다시 hello() 나 goodbye()를 사용할 수 있다.
매트릭스 문제를 다루어 보자.
첫째는 다음의 2원1차 연립 방정식의 해를 구해 보자.
이 연립 방정식은 매트릭스 형으로 다음과 같이 Cx = D로 표현할 수 있다.
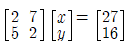
NumPy 라이브러리의 linalg.solve 명령을 사용하여 해 x 를 구하고 출력해 보자.
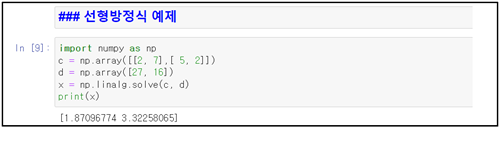
※ 매트릭스 사용과 관련하여 자주 나타나는 Determinant 계산 명령은 linalg.det(A) 임을 참조하자.
두 번째로 주어진 매트릭스에 대해 고유치(eigenvalue)를 계산해 보자.
참조: NumPy: Eigenvalues & Eigenvectors
https://scriptverse.academy/tutorials/python-eigenvalues-eigenvectors.html
정방형 매트릭스 A 와 컬럼 크기가 동일한 컬럼 벡터를 v 라고 하자. 물론 v 의 성분들은 절대 0이 아니다. 이때 다음 관계식
Av = λv
이 성립되는 λ 값 즉 eigenvalue 값을 구해보자.
실례로 매트릭스 A 와 v 는 2X2 와 2X1 크기로 다음과 같이 주어진다.
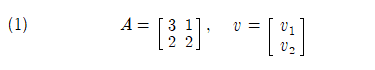
이식을 다음과 같이 조작하여 풀도록 하자.
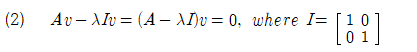
여기서 컬럼 벡터 v는 0 벡터가 아니므로 결국 (A-λI)=0 이 성립되어야 하며 이는 (A-λI) 의 Determinant 가 0 이 되어야 함을 의미한다.

NumPy 라이브러리의 linalg.eig 명령을 사용하여 eigenvalue λ 값 2개를 w로 두어 출력해 보자. λ= 4.0 과 1.0 이 얻어진다.
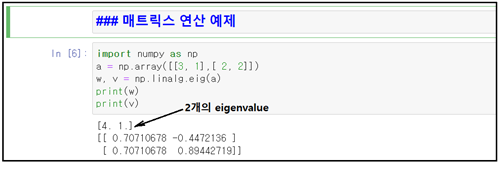
λ=1.0 을 사용하여 (2) 식에 대입해 보자.
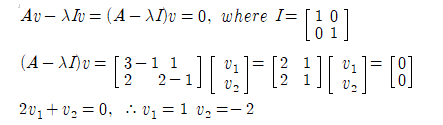
λ=4.0 을 사용하여 (2) 식에 대입해 보자.
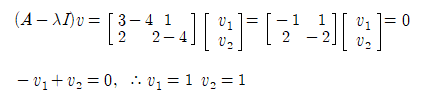
즉 eigenvalue 값에 대한 eigenvector 들이 얻어진다.
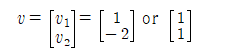
위 출력 결과의 리스트 데이터들에 대한 해석은 다음과 같이 normalization 으로 설명된다.

정방형 매트릭스 A가 3X3 크기일 때 3X1컬럼 벡터를 v 라고 하자. 물론 v 의 성분들은 절대 0이 아니다. 이때 다음 관계식
Av = λv 이 성립되는 λ 값 즉 eigenvalue 값은 3개가 계산될 수 있다.
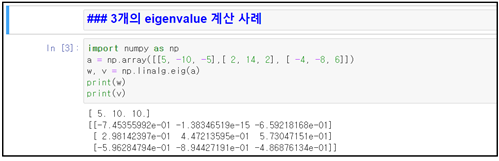
연습문제: 매트릭스 A 와 v 는 2X2 와 2X1 크기로 다음과 같이 주어질 때 eigenvalue 와 eigenvector 를 계산하여라.
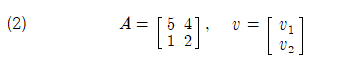
첨부된 쥬피터 파일을 다운받아 실습해 보자.
'Python' 카테고리의 다른 글
| 리눅스 폴더 구조와 구글 마운팅 (0) | 2022.08.15 |
|---|---|
| Jupyter Notebook Tutorial: 파이선 코딩 응용실습 (0) | 2022.07.26 |
| 파이선 파형 그래프 작성 기초예제 (0) | 2021.12.26 |
| 파이선 Matplotlib 오실로스코프 듀티 파형 FFT 애니메이션 예제 V (0) | 2021.12.26 |
| 파이선 Matplotlib 오실로스코프 FFT 애니메이션 예제 IV (0) | 2021.12.25 |