머신 러닝의 softmax classifier가 볼츠만 확률분포를 차용한 것 추정하지만 함께 사용되는 cost 함수인 cross entropy의 특성도 살펴보자.
일어날 가능성이 높다는 뜻의 Probable 이란 용어는 Probability의 형용사인 듯하다. Most probable Boltzmann distribution 즉 가장 일어날 확률이 높은 볼츠만 분포인데 그 뜻을 살펴보자. 볼트만 분포에서 얻어낼 수 있는 코어는 즉 macrostate j 상태에서의 microstate 의 수 Wj이다. 이 경우의 수 Wj는 어느 macrostate j 상태에서 에너지 레벨 별로 몇 개의 입자들이 분포하게 되느냐에 따라 , 즉 아래에서도 별도로 기호 설명이 있겠지만, 입자수 분포를 나타내는 nj(Ei)에 영향을 받게 되는데, 일정한 값의 상수인 총 입자수 N으로 나누어주면 입자수의 확률 분포 pi가 얻어진다. 요약하면 Wj는 확률 pi함수가 된다는 것이다.
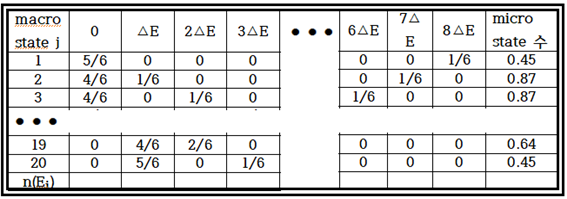
고려하는 입자 수와 에너지 레벨 수가 그리 크지 않은 경우 즉 입자 수 6, 에너지 레벨 9단계 정도는 이미 표 작성이 가능하였다. 하지만 그 숫자가 늘어난다면 오늘 날에도 쉽지 않은 주제이다. 우리가 바로 접하고 있는 머신 러닝 MNIST 문제가 바로 그런 것이다. 등가적인 의미에서 비교를 해 보자면 픽셀 수가 28X28=784 이고 에너지 레벨이 흑백 명암 기준 0∼256까지이므로 극단적인 예를 들면 784! 이라는 만만치 않게 큰 숫자가 튀어 나올 수 있다.
아래에 기술된 내용에 수식 유도와 관련되어 어려워 보일 수도 있는 표현이 많이 들어 있지만 꼭 수학포기 증상을 일으킬 필요는 없으며 정성적으로 어떤 의미인지 정도만 파악하면 될 것이다.
특정 Macrostate j에서 볼츠만의 microstate의 수를 Wj 라 하고 자연로그를 취해서 전체 입자 수 N으로 나누자. 이때에 Stirling 의 공식을 사용하도록 한다. Stirling 의 공식은 N의 값이 대단히 클 때에 N! 의 자연로그 값은 NlnN-N 으로 간단하게 근사될 수 있음을 나타낸다. 앞에서 작성 했던 표로부터 N의 값은 6 이므로 사실 그다지 큰 수가 아님에 유의하자. 간명한 표기를 위해서 nj(Ei)를 nji 로 나타내기로 한다.

이 식의 마지막 부분을 유도함에 있어서 다음의 관계식들이 사용되었다.

특정 Macrostate j에서 에너지 레벨 Ei에 입자가 가장 있을 법한 확률을 pi 로 나타내면 다음과 같이 볼츠만의 엔트로피는 입자 분포 확률함수를 사용하여 표현된다.

볼츠만 분포에 있어서 엔트로피로 정의되는 klnWj 는 용기 내부에 포함된 수많은 입자들이 가장 일어날 법한 microstate의 경우의 수로부터 확률계산에 의해 얻어지는 값이다. 앞서 구했던 에너지 레벨별 입자 분포 표에서 총입자수 N으로 나누면 아래와 같이 확률표가 얻어진다.
아울러 볼츠만 분포에서 항상 따라 다니는 볼츠만 상수 k는 거시적인 이상기체의 열역학 관계식으로부터 결정된다. 용기 내의 압력 P, 부피 V, 기체 입자들의 mole 수를 n, 가스상수를

, 절대 온도를 T 라고 하면 다음과 같이 이상기체의 상태 방정식을 쓸 수 있다.

위 식에서 용기 내에 포함된 총 입자수 N을 아보가드로수 (6.02X1023 mol-1)로 나누면 몰수가 되며, 결국 볼츠만 상수 k는 가스상수 R을 아보가드로수로 나눈 값이 됨을 알 수 있다.
볼츠만의 엔트로피 공식에서 확률 항만 남도록 볼츠만의 엔트로피 식을 아래와 같이 정리하자. pi 가 확률이므로 다음 식은 -lnpi 에 대한 기대 값 계산 정의와 유사한 형태이다.
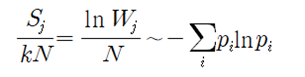
이 식에서 Σ에 포함된 부분이 바로 볼츠만의 엔트로피 공식에 해당한다.
볼츠만의 기체입자 모델에서 입자들의 에너지 레벨 분포가 양 극단 즉 영이가나 아니면 최대 값을 가질 경우에 균일한 에너지 레벨 분포에 비해 엔트로피 값이 작아지게 진다. 따라서 입자들이 여러 에너지 레벨에 골고루 분산되어 있는 경우에 엔트로피 값이 최대가 됨을 알 수 있는데 물리적으로는 이러한 상황이 바람직스럽다고 한다. 즉 볼츠만 확률 분포를 사용함에 있어 이와같이 엔트로피를 최대화 해야 하는 특성은 반대로 정보를 다루는 Shannon 의 엔트로피를 사용하는 경우와 개념적으로 큰 차이를 보일 수 있다. 즉 볼츠만 엔트로피와 수학적인 모양은 동일한 Shannon의 정보 엔트로피는 최소화 되어 Uncertainty가 최대한 제거될 경우 인식률이 100% 가까이 얻어질 수 있게 된다.
이와 같이 확률함수 pi를 이용한 물리적인 볼츠만 분포의 엔트로피 계산식의 아이디어로부터 머신 러닝의 cost 함수로 알려진 cross entropy 설정 방법과 접점을 살펴보자.
확률 pi 가 0에 가까울수록 lnpi의 값은 무한대로 커지지만 L’Hospital 정리에 의하여 -pilnpi⤍0이
극한 값을 가지며 반대로 확률 pi 가 1에 가까워지면 0에 근접한다.

볼츠만 엔트로피 공식의 –pilnpi에서 앞부분의 확률 pi를 델타함수 δi로 변경하자. 물론 델타함수 δi도 확률 pi와 마찬가지로 합이 1인 일종의 확률 분포 함수로 볼 수 있다. 한편 델타 함수는 한 지점에 집중된 형태의 분포함수로서 예를 들면 다음과 같이 정규 분포 형태의 함수를 사용하여 표현 할 수도 있는데

실수 전체 구간에서 δ(x) 함수를 적분하되 ε을 0으로 보내는 극한을 취하면 적분 값이 1.0 이 된다. 아울러 임의의 연속 함수 f(x) 에 대하여 δ(x-a)를 곱한 후 적분하여 ε을 0으로 보내는 극한을 취할 경우에도 아래와 같이 f(a) 함수 값이 얻어진다.

이와 같이 x=a에서 델타함수를 적용하면 함수 f(x) 의 x=a 에서의 함수 값이 얻어진다. 델타함수의 사용은 연속적인 경우뿐만 아니라 이산적인 경우에도 적용이 가능하다. 이산적인 경우에는 특정 위치에 있는 함수 값만을 그대로 뽑아낼 수 있게 된다.
한편 머신 러닝에서는 확률분포 pi 대신 델타 함수형의 확률로 볼 수 있는 one hot code에 따른 라벨 데이터 Y를 사용하여 cost 함수 계산을 위한 cross entropy를 다음과 같이 pointwise product 연산자 “∙”를 사용하여 표현한다.

iteration 학습 과정을 통해서 라벨 데이터 Y 와 –ln(pi )를 곱하면 라벨 데이터 1이 들어 있는 위치와 매치되는 –ln (pi )값만 얻어지고 나머지 항은 값들이 영이 되므로 다 합산하면 이 연산 과정이 –ln(pi )에 대한 델타 함수 연산이 되며 아래와 같이 표현이 가능하다.

델타함수 δji에서 j와 i가 동일하면 1이고 아니면 영이다.
즉 cross entropy를 cost 함수로 사용할 수 있으려면 –ln (pi )가 확률 pi 가 0에 가까워질수록 페널티로 무한대로 커지면서 반대로 확률 pi 가 1에 가까워지면 영에 근접하므로 cost 함수로서의 특성을 가지는 것으로 볼 수 있다.

cross 엔트로피 공식에 포함되어 있는 –ln (pi )는 분명 볼츠만 엔트로피 공식에서 차용한 것으로 보이나 one hot code 로부터 얻어지는 라벨 데이터 Y가 곱해진 cross 엔트로피는 Y 성분들의 델타함수 역할을 통해 머신 러닝의 cost 함수의 최소화를 가능하게 한다.
비록 확률분포 게산을 위해 softmax classifier를 사용한다 하드라도 cross 엔트로피 함수만이 cost 함수가 될 수 있는 것만은 아니다. 최소 제곱법도 적용이 가능하다. 이때에는 softmax 확률 값과 라벨 데이타값의 차이의 제곱 평균이 cost 함수가 된다.
첨부된 MNIST_01.py 코드를 TensorFlow 1.15.0 이나 그 이하 버전에서 실행해서 cross entropy 방식을 적용한 결과와 최소제곱법을 적용한 결과와 인식률 차이를 살펴보자.
아래에서처럼 두 줄의 코드만 수정해 주면 된다.

MNIST 코드는 매 번 실행 때마다 batch 용 샘플을 임의로 추출하기 때문에 그 값이 조금씩 변동됨에 유의하자. 실행 결과 cross entropy 모델이 최소제곱법에 비해 약 5% 인식율이 높은 것을 알 수 있다.
#MNIST_01.py
# MNIST 데이터를 다운로드 한다.
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)
# TensorFlow 라이브러리를 추가한다.
import tensorflow as tf
# 변수들을 설정한다.
x = tf.placeholder(tf.float32, [None, 784])
W = tf.Variable(tf.zeros([784, 10]))
b = tf.Variable(tf.zeros([10]))
y = tf.nn.softmax(tf.matmul(x, W) + b)
#y = tf.nn.sigmoid(tf.matmul(x, W) + b)
# cross-entropy 모델을 설정한다.
y_ = tf.placeholder(tf.float32, [None, 10])
#cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))
#train_step = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cross_entropy)
cost = tf.reduce_mean( tf.square(y-y_))
train_step = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# 경사하강법으로 모델을 학습한다.
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(20000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
# 학습된 모델이 얼마나 정확한지를 출력한다.
correct_prediction = tf.equal(tf.argmax(y,1), tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
print(sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
'머신러닝' 카테고리의 다른 글
| 2-14 Sigmoid vs softmax 확률분포 비교: Rosenblatt 퍼셉트론 N = 1 (0) | 2021.06.30 |
|---|---|
| 2-1 softmax 머신러닝 다음 주제로 Rosenblatt의 퍼셉트론(1957)을 살펴보자. (0) | 2021.06.28 |
| 1-26 Irises flower(붓꽃) dataset 텐서플로우 머신 러닝 (0) | 2021.06.27 |
| 1-25 볼츠만 확률 분포에서의 Random 변수와 조건부 확률분포 (0) | 2021.06.27 |
| 1-24 볼츠만, Bose-Einstein, Fermi-Dirac 확률분포와 머신러닝 classification 과의 유사성 (1) | 2021.06.27 |