softmax classifier를 사용하는 머신 러닝 문제에서 갑자기 붓꽃 종 분류(Classification of Iris flowers ) 문제가 제기된 이유를 알아보자. softmax 문제의 가장 적합한 예제는 물론 MNIST 수기숫자 인식 파이선 코드를 사용하면 될 일이겠지만 단지 softmax의 원리를 설명함에 있어서 28X28=784 픽셀 이미지 5만개를 학습에 사용하는 MNIST 예제는 웬지 적절해 보이지 않는다. 그렇다고 해서 임의로 만든 의미 없는 숫자 데이터를 사용한다면 softmax 코드 설명은 가능하겠으나 classification을 공부하는 의미가 퇴색된다.
따라서 softmax 수치 예제로서 그 원리 설명에 가장 적합한 예제는 클라스 또는 라벨 수가 적을수록 좋을 듯하니 바이오 통계학 분야의 권위자였던 Fisher 교수와 식물 발생학 분야의 전문가였던 하버드의 Anderson 교수가 무려 80년 전 즉 1936년에 붓꽃 종 분류를 위해 준비해둔 데이터를 가져다 쓰기로 한다.
Setosa, Versicolor, Verginica 3종의 붓꽃 데이터는 Wikipedia Iris flower data set의 아래 인터넷 주소에서 참고할 수 있다.
https://en.wikipedia.org/wiki/Iris_flower_data_set
150개의 데이터 중에서 각 종 별로 3개씩의 데이터를 취해서 학습용으로 사용하고 뒤따르는 데이터 1개씩을 취해서 테스트용으로 사용하기로 한다. 각 데이터의 치수는 Iris 꽃의 치수 구성도를 참조한다.

따라서 이어지는 softmax classifier 사용법 설명 후 Fisher의 붓꽃 데이터를 12개를 취해 사용하는 첨부된 코드를 실행해 보면 무려 80년이 경과된 데이터이긴 하지만 붓꽃에 아직 돌연변이가 나타나지 않은 이상 뭔가 생생한 느낌을 맛볼 수 있을 것으로 기대한다.
Iris flower data를 사용한 softmax classification 예제 코드의 헤더 영역을 살펴보자.

random_seed를 사용하면 코드 재실행 시 항상 동일한 결과를 받아 볼 수 있게 된다. 4개의 원소를 가지는 리스트 형태의 입력 데이터 x_data 는 iris 꽃 종류별로 3개씩 총 9개를 사용한다.
3개의 원소를 가지는 리스트 형태의 입력 데이터 y_data 는 분류용 데이터로서 또는 label 이라고도 하는데 one hot code를 사용한다. 3가지 종류의 iris 꽃 종류를 다루기 위한 one hot code로서 숫자로 “0”,“1”,“2” 를 대응시킨 후 아래와 같이 one hot code를 리스트 형태로 정의한다. 아래의 그림을 참조하자. MNIST에서 처럼 구별해야 할 종류가 0∼9까지의 십진 숫자라면 점을 찍은 박스가 10칸이 되고 그 아래의 리스트 데이터도 10자리가 되어야 할 것이다. 한편 one hot code는 확률적인 의미도 함께 가지는데 그 합이 1.0 이란 점이며 해당 위치에서만 1이고 나머지 위치에서는 0이므로 수학적으로 델타 함수에 해당한다.

one hot 코드를 적용해 보면 y_data의 각 label들은 아래와 같이 됨을 알 수 있다.
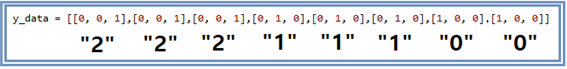
placeholder는 Session에서 batch를 실행하기 위해서 필요한 변수들의 메모리를 미리 잡아 놓는 역할을 한다.
이 Iris 꽃 종류별 학습에 의한 수치 예제에서는 x_data 리스트 데이터 수만큼의 y_data 가 있음을 알 수 있다. 즉 x_data 수가 None 이면 y_data 수도 None 으로 처리해야 한다. 즉 입력 데이터 수가 몇 개이든 서로 같은 수를 매치시키도록 하면 된다. None 으로 처리해 두고 Session에서 직접 필요한 숫자를 지정하면 되며, 참고로 MNIST 의 경우 6만개의 샘플에서 100개씩 batch 단위로 샘플하여 계산을 수행한다.
변수 nb_class 는 앞에서 3 종류로 분류하기로 하였으므로 3으로 둔다.

입력 데이터가 4개의 실수형 원소를 가지므로 1X4 matrix 형 리스트 데이터로 볼 수 있다. 따라서 웨이트를 4X3 matrix로 설정하면 계산 결과 3개의 원소를 가지는 리스트 데이터가 나오므로 여기에다 3개의 원소를 가지는 편향(바이어스) 리스트 데이타를 더하면 최종 3개의 원소를 가지는 리스트형 데이터가 얻어지는데, 각각의 원소에 대해서 아래와 같이 softmax 명령을 적용하여 hypothesis 를 계산한다.

hypothesis를 한번 계산하면 위 계산 예처럼 3X1 matrix 가 얻어지며 이들은 확률분포이므로 합이 반드시 1.0 이 되어야 한다. 이와 같은 머신 러닝 과정에서 아무리 입력 데이터가 많아도 이 문제에서의 웨이트 W는 4X3 matrix 이며 아울러 1X3 편향(바이어스) matrix 와 함께 cost 함수의 최소화를 위한 경사하강법을 적용하고 iteration 과정을 통해 결정된다.
이와 같이 입력 데이터 x_data와 학습의 답에 해당하는 라벨 데이터 또는 클라스 데이터 y_data 가 준비 되었으면 hypothesis 와 cost 함수를 구성하여 적절한 값의 learning rate를 설정해서 경사하강법을 적용하여 필요한 횟수만큼 iteration을 시키도록 한다. 이 과정을 학습(trainning)과정이라 한다. 입력에 대한 정답(라벨, 클라스 데이터)을 준 상태에서 경사하강법에 의해 hypothesis 에 포함되어 있는 웨이트 W 와 편향(바이어스) b를 결정할 수 있다.
softmax 수치 예제 문제에서 cost 함수의 형태에 주목하자. 머신 러닝 선형 회귀 문제를 정식화함에 사용하는 최소자승법(제곱법, least square method)에서는 모든 입력 데이터에 대하여 (라벨 값 - hypothesis)의 제곱 항을 더해 평균을 낸 후 경사하강법에 의해 웨이트 W 와 편향(바이아스) b를 결정한다. 반면에 softmax classifier를 사용하는 문제에서는 최소제곱법과는 또 다른 형태의 cross entropy 로 명명되는 cost 함수가 구성되어 사용된다. 아래는 파이선 언어로 표현된 cost 함수이다.

이 cost 함수의 구체적인 내용을 이해하기 쉽게 아래와 같이 다시 써보자.

y로 표현된 hypothesis는 softmax classifier 명령을 사용하여 3X1 matrix 형태의 확률분포로 계산 된다. 한편 cost 함수는 one hot code인 클라스 또는 라벨 데이터로서 2개가 0의 값을 가지고 1개만 1이 된다. 위 그림에서 사용된 연산자 “∙”는 pointwise product 또는 Hadamard product로 불리운다. 만약에 라벨 데이터 Yi를 확률분포 pi 로 대체하면 아래와 같은 형태가 됨을 알 수 있다.

이 식에서 Σ에 포함된 부분이 바로 그 유명한 볼츠만의 또는 Shanon의 엔트로피 공식에 해당한다. 하지만 머신 러닝에서는 확률분포 pi 대신 델타 함수형의 확률로 볼 수 있는 라벨 데이터로서 one hot code를 사용하며 cost 계산을 위한 cross entropy 로 명명한다.

확률 pi가 0으로 가게 되면 - ln pi 값이 +∞가 되고 확률이 1에 접근하면 값이 0이 되는 아래 그래프와 같은 특성을 보여 준다. 아울러 확률이 0으로 가드라도 0∙(+∞) 되는 부분은 L’Hospital의 미분 공식에 의해서 0이 됨을 알 수 있다. 학습이 이루어짐에 따라 확률 pi가 우리가 답을 알고 있는 one hot code 형태의 클라스 라벨 데이터에 근접하게 된다. 아래와 같은 상황을 예로 고려해 보자.

첫 번째 데이터 세트에서 0.7이 가장 큰 확률 값이므로 자연 로그를 취하면 가장 작은 값이 되며 라벨 데이터 Y값 1을 pointwise product 하면 3개 중 최소값이 얻어지며 나머지 2개는 0이 된다. 나머지 데이터 세트에서는 두 번째와 세 번째가 3개 중 최소값이 된다. 학습과정에서 learning rate 값이 적절하다면 iteration 진행에 따라 라벨 값에 확률값 pi가 얼마든지 가까워 질 수 있다. 물론 cost 함수로서 cross entropy 말고도 최소제곱법을 적용해 최종 인식율을 계산해 보면 정밀도가 한참 못 미친다는 점을 쉽게 알 수 있디.
얼마나 학습이 잘되었는지 결과를 정답을 알고 있는 경우를 대상으로 테스트해 보자. 즉 아래 예에서는 Fisher’s Irsis data 표의 4번 setosa 데이타인 [4.6, 3.1, 1.5, 0.2]를 대입하여 학습과정에서 계산해둔 웨이트와 편향값을 사용하여 hypothesis 값을 구해 a 라 두고, argmax(a,1) 명령을 사용하여 3X1 데이터 중 제일 큰 값이 몇 번째인지 체크해 보자.

아래는 softmax_classifier_9data_iris_01.py 파이선 코드를 실행해 나온 결과이다. 계산 결과를 보면 cost 함수가 적절하게 감소하고 있다.

아래의 출력 결과에서 3개짜리 리스트 데이터는 softmax 처리된 hypothesis의 리스트 데이터 3개를 출력한 결과이며 뒤 따르는 [ ] 은 확률 값이 제일 큰 위치를 argmax(a,1) 로 찾아낸 값이다. 앞에서 설명한내용이 적절한 숫자 표현으로 제시된 듯하다. 이 문제의 해답은 각각 [0]=Iris-setosa, [1]=Iris-versicolor, [2]=Iris-virginica 이다.

이로서 softmax classifier를 사용하는 텐서플로우 머신 러닝에 의해서 실제 붓꽃 데이터를 가지고 성공적으로 종류별 분류를 하였다. 한편 붓꽃은 식물 종 분류의 대상 이전에 반 고호의 관심을 끌었던 꽃 중에서 해바라기를 제외한 그 자태가 아름다운 꽃으로서 유니크한 사생 대상이기도 하였다.(1889)

첨부한 코드를 각자 실행해 보자.
#softmax_classifier_9data_iris_01.pyimport tensorflow as tf
tf.set_random_seed(777) # for reproducibility
x_data = [[5.1, 3.5, 1.4, 0.2], [4.9, 3.0, 1.4, 0.2], [4.7, 3.2, 1.3, 0.2],
[6.4, 3.2, 4.5, 1.5], [6.9, 3.1, 4.9, 1.5], [5.5, 2.3, 4.0, 1.3],
[5.8, 2.7, 5.1, 1.9], [7.1, 3.0, 5.9, 2.1], [6.3, 2.9, 5.6, 1.8]]
y_data = [[1, 0, 0], [1, 0, 0], [1, 0, 0],
[0, 1, 0], [0, 1, 0], [0, 1, 0],
[0, 0, 1], [0, 0, 1],[0, 0, 1]]
X = tf.placeholder("float", [None, 4])
Y = tf.placeholder("float", [None, 3])
nb_classes = 3
W = tf.Variable(tf.random_normal([4, nb_classes]), name='weight')
b = tf.Variable(tf.random_normal([nb_classes]), name='bias')
# tf.nn.softmax computes softmax activations
# softmax = exp(logits) / reduce_sum(exp(logits), dim)
hypothesis = tf.nn.softmax(tf.matmul(X, W) + b)
# Cross entropy cost/loss
cost = tf.reduce_mean(-tf.reduce_sum(Y * tf.log(hypothesis), axis=1))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.1).minimize(cost)
# Launch graph
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for step in range(2001):
sess.run(optimizer, feed_dict={X: x_data, Y: y_data})
if step % 200 == 0:
print(step, sess.run(cost, feed_dict={X: x_data, Y: y_data}))
print('--------------')
# Testing & One-hot encoding
a = sess.run(hypothesis, feed_dict={X: [[4.6, 3.1, 1.5, 0.2]]})
print(a, sess.run(tf.argmax(a, 1)))
print('--------------')
b = sess.run(hypothesis, feed_dict={X: [[5.5, 2.3, 4.0, 1.3]]})
print(b, sess.run(tf.argmax(b, 1)))
print('--------------')
c = sess.run(hypothesis, feed_dict={X: [[6.3, 2.9, 5.6, 1.8]]})
print(c, sess.run(tf.argmax(c, 1)))
print('--------------')
all = sess.run(hypothesis, feed_dict={
X: [[5.0, 3.6, 1.4, 0.2],[6.5, 2.8, 4.6, 1.5],[6.5, 3.0, 5.8, 2.2]]})
print(all, sess.run(tf.argmax(all, 1)))
'''
--------------
[[ 1.38904958e-03 9.98601854e-01 9.06129117e-06]] [1]
--------------
[[ 0.93119204 0.06290206 0.0059059 ]] [0]
--------------
[[ 1.27327668e-08 3.34112905e-04 9.99665856e-01]] [2]
--------------
[[ 1.38904958e-03 9.98601854e-01 9.06129117e-06]
[ 9.31192040e-01 6.29020557e-02 5.90589503e-03]
[ 1.27327668e-08 3.34112905e-04 9.99665856e-01]] [1 0 2]
'''
'머신러닝' 카테고리의 다른 글
| 2-1 softmax 머신러닝 다음 주제로 Rosenblatt의 퍼셉트론(1957)을 살펴보자. (0) | 2021.06.28 |
|---|---|
| 1-27 softmax 머신 러닝의 cross entropy vs least square cost 함수 (0) | 2021.06.28 |
| 1-25 볼츠만 확률 분포에서의 Random 변수와 조건부 확률분포 (0) | 2021.06.27 |
| 1-24 볼츠만, Bose-Einstein, Fermi-Dirac 확률분포와 머신러닝 classification 과의 유사성 (1) | 2021.06.27 |
| 1-23 Microstate 수로부터 유도하는 볼츠만 확률분포 공식과 softmax classifier (0) | 2021.06.26 |