양자 알고리듬 첫번째 관문: Deutsch–Jozsa algorithm

 

 

Step by step guide to Deutsch's Algorithm

https://www.jonvet.com/blog/math-behind-deutsch-algorithm

 

 

※ The Deutsch-Jozsa Algorithm — Math, Circuits, and Code: Quantum Algorithms Untangled

https://medium.com/quantum-untangled/the-deutsch-jozsa-algorithm-math-circuits-and-code-quantum-algorithms-untangled-f3b28be4cfd3

 

 

 

 

개론

 

모든 확률 분석은 주사위 놀이나 동전 던지기 같은 게임에서 비롯된다. 이 원리는 양자 컴퓨팅에도 필연적으로 적용되지만, 양자 컴퓨팅 환경에서의 야바위 게임의 경우, 그 의미와 본질이 크게 달라지는데, 바로 이 문제를 다루는 과제가 도이치 알고리즘이다.

 

이런 동전 던지기 게임 자체가 야바위스랍게 느껴지기때문에 양자 컴퓨팅의 도이치 알고리듬은 더 한층 야바위성이 강한 그런 주제에 해당한다. 과연 어떤 작자들이 이 수학적인지 물리학적인지 조차 분명치 않은 문제를 연구했는지 정신 상태가 상당히 의문스러웠는데 자료를 찾다보니 1992년에 물리학자 출신들인  Deutsch 와 Jozsa 가 연구 결과를 제시하였다. 참고로 그 당시에 양자 컴퓨터 조차 없았는데 무슨 연구 실적을 내려고  그랬는지 읽어 보면 이해하기 쉽지 않은 측면이 있어 보인다.

 

그래도 양자 컴퓨팅 알고리듬 공부에서 피할 수 없는 첫번째 관문이기에 어쩔수 없이 다루어 보도록 하자.  설혹 읽어 본 후에도 뭔 소린지 모르겠다 라는 경우에도 그러려니 하고 다음 관문으로 넘어가길 바란다. 그렇다면 두번째 관문은 무엇일까? 우리말로는 "건초더미에서 바늘찾기"인데 그루버 알고리듬이라 한다. 세번째로는 거대한 정수의 소인수 분해 문제로서 이 문제 해결시 비트코인 암호화폐 비밀번호 해독도 가능해진다. 즉 세번재 문제의 성공은 세상이 바뀔 수도 있다는 점이다.

 

문제 서술

 

도이치 알고리즘에서의 입력과 출력 0 과 1 은 동전 던지기 게임에서 앞면과 뒷면을 나타낸다고 가정하자. 0 또는 1 을 입력 변수로 하여 출력도 0 또는 1 을 반환하는 함수 f(x)가 있을 때, 이 함수가 상수 함수인지 균형 함수인지 판별해 보도록 하자. 

 

동전 던지기 도박에서는 항상 앞면과 뒷면이 입력값이 될 수 있으며 출력값 또한 항상 앞면과 뒷면이 된다. 따라서 그러한 함수 f(x) 는 존재하지만 함수의 구체적인 형태는 알 수 없다. 야바위 게임의 경우 항상 남을 등쳐먹어야 하므로 함수를 일정한 패턴으로 조작이 가능해야 하지만 진정한 확률 게임이라면 함수 자체를 알아내서 식으로 쓰기는 불가능하다고 볼 수 있다.

 

상수 함수는 입력값에 무관하게 출력값이 항상 0 이거나 항상 1 인 함수를 의미한다. 균형 함수는 한 입력값에 대해서 출력값이 0이면 다른 입력값에 대해서는 반드시 1인 함수이다.

 

함수가 단일 비트(0 또는 1)를 입력으로 받기 때문에 가능한 함수는 다음 4가지뿐이다.

 

2가지 가능한 함수는 상수 함수이다

1.1 f(0)=0 및 f(1)=0 이면 f 는 상수 함수

1.2 f(0)=1 및 f(1)=1 이면 f 는 상수 함수

 

2. 나머지 가능한 함수는 균형 함수이다.

2.1 f(0)=0 및 f(1)=1 이면 f 는 균형 함수

2.2 f(0)=1 및 f(1)=0 이면 f 는 균형 함수

 

도이치 알고리듬 문제는 주어진 함수의 출력 결과가 상수인지 균형인지를 결정하는 문제로서 고전적인 관점에서 보면 XOR 논리 문제와 유사하다. 동전 앞면과 뒷면을 입력으로 던질 때 둘 다 앞면이 나오든가 또는 둘 다 뒷면이 나오든가 아니면 하나는 앞면 다른 하나는 뒷면 또는 하나는 뒷면 다른 하나는 앞면이 나오는 경우로서 XOR 논리를 나타낸다.

 

The Classical Solution involves 2 queries.

 

고전적인 해결 방법은 두 번의 쿼리(query)를 필요로 한다.

이 문제를 고전적인 방식으로 접근하면 함수 f 가 상수 함수인지 균형 함수인지 판별하기 위해 반드시 두 번 호출해야 한다는 것을 쉽게 알 수 있다.

 

예를 들어, 입력값 0으로 함수를 호출하여 출력값이 1 이라면 f(0)=1 임을 알 수 있다. 즉 f(0)=1 이면, 1.2번 경우(상수 함수) 또는 2.2번 경우(균형 함수) 중 하나임을 알 수 있다.

 

하지만 두 경우를 구분하기 위해서는 입력값 1 로 함수를 한 번 더 호출해야 한다. 고전적인 관점에서 상수인지 균형인지 확인하려면 0 과 1을 각 1회씩 합 2 회를 던져서 결과가 1.1, 1.2, 2.1, 2.2 중에 어느 하나인지 확인해야 한다. 이러한 의미에서 고전적인 해는 2회의 쿼리(query)를 사용하는 셈이다.

 

The Quantum Solution by Deutsch Algorithm involves just 1 queries.

 

반면 도이치 알고리듬에 의한 해법은 다음의 원리에서처럼 단 하나의 쿼리만을 사용하여 해결이 가능하다는 점이다.

중첩: 큐비트 하나를 중첩 상태로 만든 다음 f(x) 를 적용한다. 이는 일시에 2개의 입력값 적용을 가능하게 한다.

 

위상 kickback: CNOT 게이트와 같이 제어된 양자 게이트 연산 중에 큐비트의 위상이 다른 큐비트로 "kickback"되는 현상이다. 아래의 설명에서 kickback 의 구체적인 내용을 파악하자.

 

Deutsch 알고리듬 개요

양자 상태 |0> |1> 에 해당하는 큐비트 x 와 y 를 준비하고 이들을 |φ>0로 둔다.

2개의 큐비트에 아다마르 게이트를 각각 적용하여 중첩 상태에 두고 |φ>1 으로 두자.

3. 4지 선택이 가능한 각 경우의 함수 f 에 대해 함수 Uf 를 적용하여 |φ>2 로 둔다.

4. 큐비트 x 에 아다마르 게이트를 적용하여 |φ>3 로 두자.

5. 큐비트 x 를 측정한다.

 

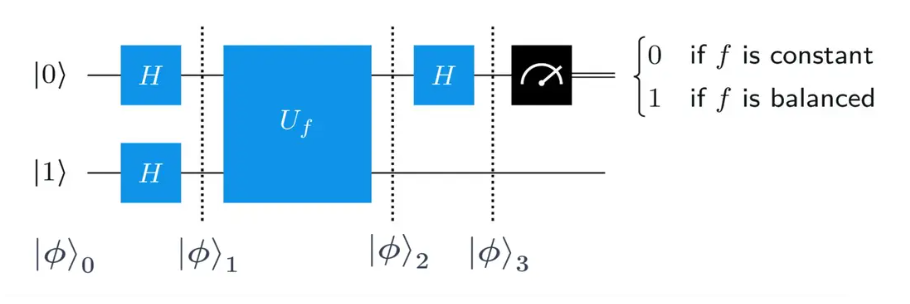
함수 f 가 상수 함수이면 측정값은 항상 0 이 된다. 균형 함수이면 측정값은 1 이 된다. 중요한 것은 이 함수를 한 번만 호출하면 된다는 점이다. Deutasch 알고리듬을 실행하기 위한 양자 회로는 다음과 같다.

XOR 연산자/모듈로 2 덧셈

XOR 연산자는 배타적 논리합(XOR) 또는 모듈로 2 덧셈이라고도 하며, 두 비트를 입력받아 서로 다르면 1, 같으면 0을 반환하는 이진 연산이다. XOR 연산자는 기호 ⊕로 나타낸다.

 

예를 들어, 4 ⊕ 2는 이진수 100 과 010의 XOR 덧셈 연산 결과를 의미하며, 이진수 110(십진수 6) 이 된다.

                                                 100

                                                 010

                                               --------

                                                 110

 

문제 서술에서 얻어진 4개의 결론 1.1 ~ 2.2 는 XOR 논리를 사용하여 다음과 같이 2개의 경우로 압축이 가능하다, 

 

f(0) ⊕ f(1) = 0 이면 상수함수 (※ 1.1 과 1.2 를 통합)

f(0) ⊕ f(1) = 1 이면 균형함수 (※ 2.1 과 2.2 를 통합)

 

※ f(0) 나 f(1) 의 값들이 0 또는 1 이되는 경우는 앞면 또는 뒷면을 뜻하지만 XOR 논리 연산 결과로서 0 또는 1 인 결과는 거짓(False, 상수함수)) 또는 참(True, 균형함수)을 뜻하므로 혼동되지 않도록 주의하자.

 

이렇게 압축된 결과는 최종 단계에서 큐비트 붕괴에 의한 측정 단계에서 양자 컴퓨팅 결과로 얻어질 수 있음에 유의하자.

 

 

Introducing a controlled quantum operation

 

Deutsch 알고리듬은 2개의 큐비트를 수반한다. 하나는 f(x) 평가를 위해 호출하는 큐비트 x 이며, 다른 하나는 위상 ”kickback“에 사용하는 큐비트 y 이다.

첫째로, 가역적이면서 unitary 특성을 가지며, 함수 f(x) 를 큐비트 x 와 y 에 적용하는 2큐비트 전담 게이트 Uf 로 정의되는 이는 오직 본 블로그의 Deutsch 알고리듬 문제에만 딱 한번 적용할 수 있으며,  Deutsch 라는 연구자가 중요하다고 보는 양자 게이트 Uf  가 있다.

 

Uf 의 역할은 큐비트 상태 ∣x ⟩와∣y ⟩를 ∣x⟩와 | y ⊕ f(x) ⟩로 매핑하는 것이다.

⊕ 기호는 XOR 논리 연산자를 뜻하며, f(x) 는 앞서 설명한 1.1 ~ 2.2 의 4 경우를 뜻한다.

 

Uf 의 적용은 f(x) 의 값에 기반하여 양자 상태 y( |y> )를 변경한다. 즉 양자 상태 x( |x>) 가 양자 상태 y( |y> ) 를 제어하는 것이다,

 

상수 함수인 f(x)=0 인 즉 x=0 이거나 1 인 경우 XOR 논리를 포함하는 Uf 가 어떻게 작용하는지 알아보자.

 

|x> |y>     |x>  |y ⊗ f(x)>

|0> |0> → |0> |0 ⊗ 0> = |0> |0>

|0> |1> → |0> |1 ⊗ 0> = |0> |1>

|1> |0> → |1> |0 ⊗ 0> = |1> |0>

|1> |1> → |1> |1 ⊗ 0> = |1> |1>

 

결과를 관찰해 보면 Uf 작용 전의 큐비트 상태에 전혀 변화가 없음을 알 수 있다.

f(x)=x 일 때 즉 x=0 이면 f(0)=0 이고 x=1 이면 f(x)=1 이 되는 균형 함수의 사례를 살펴보자.

 

|x> |y>      |x> |y ⊗ f(x)>

|0> |0> → |0> |0 ⊗ 0> = |0> |0>

|0> |1> → |0> |1 ⊗ 0> = |0> |1>

|1> |0> → |1> |0 ⊗ 1> = |1> |1>

|1> |1> → |1> |1 ⊗ 1> = |1> |0>

 

세 번째 와 네 번째 결과에 XOR 논리에 의한 변화를 관찰할 수 있다.

 

Walking through Deutsch Algorithm step by step

 

다음과 같이 2개의 큐비트 상태를 갖는 확률 파동함수 |ϕ >0 를 고려하자. ket 벡터를 연이어  즉 곱셈 상태로 둘 경우 더 이상 연산은 이루어지지 않으며 그냥 텐서 곱 형태를 유지한다. 여기서 텐서 곱은 AND 개념 정도로 이해하자.

 

|ϕ >0  = |0>  |1>

 

각 큐비트 |0> 과 |1> 에 대한 아다마르 게이트 적용하여 확률 파동함수 |ϕ >1 을 생성하여 Uf 게이트에 입력한다.

 

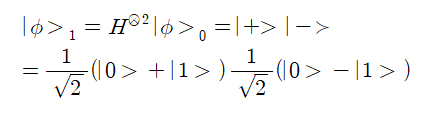
뒷 부분을 앞 부분의 각항과 곱하여 전개하면 다음 식이 얻어진다.

 

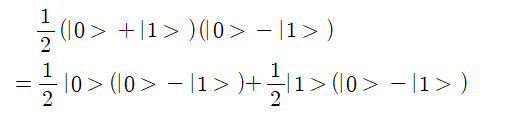
게이트 Uf를 적용하여 ∣x⟩와∣y⟩를 ∣x⟩와 | y ⊕ f(x)⟩로 매핑하자.

 

 

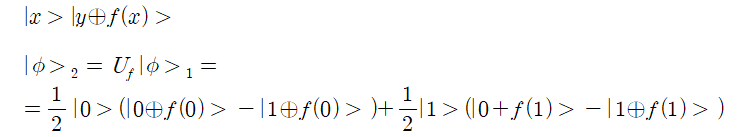
식을 간략화하기 위해서 다음 식을 사용하자. a 는 f(0) 또는 f(1) 으로서 0 또는 1 의 값을 가질 수 있다. 함수 f 는 입력 및 출력 값을 제외하고 구체적으로 정의를 알 수 없기 때문에 아래의 식은 관계식이 될 수는 없고, 일단 수치적으로 만족은 하므로 항등식이라고 하기로 한다.

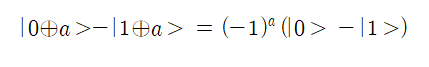
위 식을 대입하면 다음 결과가 얻어진다.

 

 

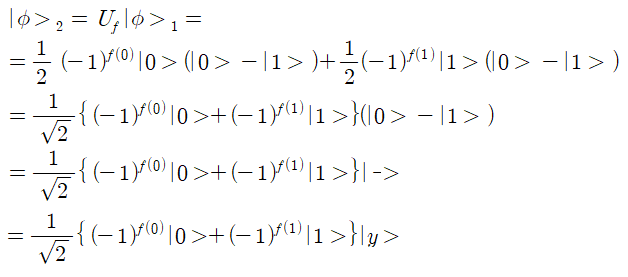
이 식을 살펴보면 Uf 적용 결과 양자 상태 |y>를 그대로 유지한 채 양자 상태 |x> 즉 |0> 의 ”kicked back the phase factor“에 해당하는 (-1)의 f(x)승을 괄호 앞으로 풀어내기 위해 다음의 항등식을 사용하면서

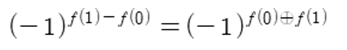
최종적으로 다음식이 얻어진다.

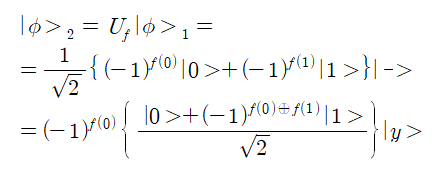
f(0) 와 f(1) 은 0 또는 1 이므로 그 차이는 0, 1, -1 이 될 수 있다. 차이가 0 이면 (-1)의 0승은 1 이 된다. 만약 그 차이가 1 또는 –1 이라면 (-1)의 –1승 이나 +1승이면 그 결과는 –1 이 된다.

 

그러므로 이 식의 제일 앞부분은 global phase 에 해당한다. (※ global 의 의미는 초전도체 죠셉슨 소자의 양자역학적 모델링 과정서 Ginzburg Landau 에 의해 복잡한 전자의 파동현상을 간략하고 정확하게 기술하기 위해 정식화시킨 single global wave function에서의 global을 의미하는 듯하다,)

 

 

여기까지 유도 후 step by step 블로그 저자로부터의 마지막 결론은 오히려 이해하기 어려운 측면이 있어, 그 대안으로 보다 단호한 결론을 보여주는 Wikipedia 의 Deutsch algoritm 의 해석 내용으로 대체하여 논의를 마무리 하고자 한다.

Deutsch–Jozsa algorithm Wikipedia

https://en.wikipedia.org/wiki/Deutsch%E2%80%93Jozsa_algorithm

 

다음 식은 앞에서 이미 유도 했던 빨간 박스친 부분에 한정하여 이 부분에 아다마르(Hadamar)연산을 실행하고 M 이라 두고 측정을 하자. 글로벌 phase 에 해당하는 (-1)의 f(0) 승은 중첩 상태 붕괴에 따른 측정 시에 별 영향이 없다고 볼 수 있다. 붕괴 시에는 복소수인 각 양자 상태 계수의 크기의 제곱의 합이 1.0 이 되는지 여부가 중요하다.

|y> 를 붕괴시켜 측정하면 |0> 이나 |1>에 대해서 1.0 의 값을 주지만 동전 던지기 f(x) 와는 아무런 관련이 없음에 유의하자. 즉 Uf 는 |x> 나 |y> 또는 f(x) 에는 아무런 영향을 미치지 않는다.

 

빨간 박스친 부분에 대한 아다마르 연산 결과는 다음과 같다.

 

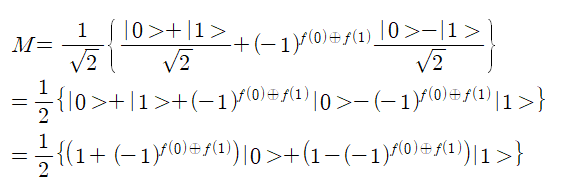
양자 붕괴를 시켜 측정을 하면 |0> 이나 아니면 |1> 의 계수만 남게 되는데 그 값이 1 이 된다.

|0> 일 경우 계수는 다음과 같이 1 이 되어야 하므로 상수함수 조건이 얻어진다.

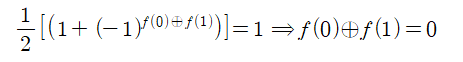
|1> 일 경우의 계수도 다음과 같이 1 이 되어야 하므로 균형함수 조건이 얻어진다.

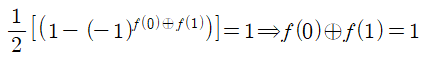
결과적으로 함수 Uf를 사용 XOR 논리를 도입하여 큐비트를 조작한 결과 고전적으로는 상수 함수인지 균형 함수인지 결정하기 위해서는 각 2회씩의 query를 해야 하지만 1회의 query 로 결과를 얻을 수 있음이 밝혀진다.

 

2개의 큐비트를 사용하는 양자 컴퓨팅에서 과연 Uf 게이트를 초전도체 죠셉슨 소자로 구성된 예를 들자면 Transmon 에서 어떻게 하드웨어를 조작할 것인가도 큰 기술적인 문제로 남는다. 만약 1 query 당 1억 년이 걸린다면 반으로 줄일 경우 5천만 년의 시간을 절감할 수 있다는 논리이다. 양자 컴퓨팅 알고리듬 문제는 다 이런식이므로 앞으로의 공부 과정에서도 지나치게 허탈감을 느끼거나 충격을 받지 않도록 조심하기 바란다.

 

Deutsch 알고리듬 qiskit 코딩은 별도의 블로그에서 다루어 보기로 한다.

 

 

 

다음 유튜브 사이트는 Deutsch Algorithm 의 복잡성으로 인해 그 수학적 내용을 생략하고 코딩만 제시한다.

어서와! 양자 컴퓨팅은 처음이지? 6. 양자 알고리듬은 왜 빠른가?

https://www.youtube.com/watch?v=kLZfqkshogw&t=735s

 

 

https://akyrillidis.github.io/notes/quant_post_8

Introduction to quantum computing: The Deutsch algorithm.