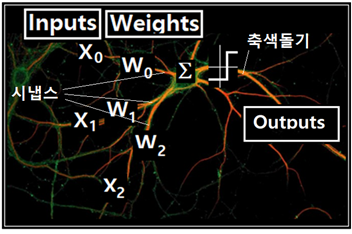
수상돌기의 시냅스 영역에서 신경전달물질(neurotransmitter) 분비를 통해 입력 신호 전달과 웨이팅이 일어나며 아울러 여러 개의 수상돌기가 연결된 뉴론에서 시그마(∑)에 의한 가감 합산이 일어난다. 합산된 전위 값은 threshold 조건 만족 여부에 따라 fire 즉 신경 충격이 일어나게 되며 뉴론에서 외부로 연결된 축색 돌기를 통해 신경 정보 전달이 이루어진다. 사진에서도 볼 수 있지만 신경망 NN(Neural Network)은 하나의 뉴론에 여러 개의 수상 돌기가 연결되기도 하며 아울러 여러 개의 축색 돌기에 의해 외부 뉴론과의 연결이 이루어진다.
물론 뉴론 내 외부에서 일어나는 복잡하고 마이크로한 생화학적인 측면을 그대로 머신 러닝을 위한 신경망으로 묘사할 수는 없으며 결국 어떤 방식으로든 모델링 처리가 필요하며 그 중 에 가장 단순한 모델이 퍼셉트론일 것이다.
퍼셉트론을 대상으로 한 AND 로직과 OR 로직머신 러닝에서는 하나의 퍼셉트론을 중심으로 입력 신호 처리, 웨이팅 그리고 시그마(∑)에 의한 가감 합산처리, threshold 판단에 따른 firing 과정에 이르기까지 별문제 없이 처리가 가능하다. 하지만 XOR 로직에 이르러서는 신호가 입력되어도 웨이팅 값이 0 이 되고 바이아스 값이 상수인 0.5로 결정되어 firing 할 것인지 말 것인지 결정이 불가능해진다. (W0 = 0.5, W1 = 0.0, W2 = 0.0) 그렇다고 간단한 구조의 퍼셉트론 모델이 특별히 고장난 것은 더더욱 아니다.
왜 이런 현상이 발생하는 것일까? 하나의 퍼셉트론이라는 조건에 유의해 보자. 간단히 말하면 XOR 로직을 처리하는데 필요한 웨이트 벡터의 수가 충분히 않아 일어나는 현상이다. 다시 말해서 충분한 수의 웨이트 벡터를 사용하면 처리가 가능하다는 점이다. 실제 생체 내에서 뉴론의 수는 10억∼100억개 또는 그 이상으로 추산되며, 그 수많은 뉴론 들이 어떤 연결 체계에 의해서 주변 환경으로부터 입력되는 신호들을 처리하는지 알아볼 필요가 있다. 즉 필요한 만큼의 교차 연결된 퍼셉트론 시스템을 대상으로 머신 러닝을 해 볼 필요가 있는 것이며 적어도 제대로 된 퍼셉트론 신경망을 구성하려면 퍼셉트론간의 firing 처리가 가능할 수 있도록 Sigmoid 함수 처리 기능도 반드시 부가되어야 할 것이다.
하나의 퍼셉트론으로 XOR 로직을 시험해 보면 분명 2개의 웨이트 벡터에 해당하는 2개의 분리선이 결정 되어야 함에도 불구하고 퍼셉트론의 원리 상 하나의 웨이트 벡터 밖에 없으므로 당연히 그다지 쓸모가 없는 trivial 한 결과가 얻어진다. 결국 2개의 웨이트 벡터를 결정하려면 2개의 퍼셉트론을 직렬이나 병렬로 구성하여 동일한 입력 벡터에 대하여 독립적으로 랜덤한 2개의 웨이트 벡터를 결정해야 한다.

그림과 같이 1세트의 입력 데이터에 대해서 퍼셉트론 2개를 사용하여 병렬로 구성하게 되면 각각의 퍼셉트론이 출력을 발생시키게 된다. 즉 서로 독립적인 웨이트 2개가 필요한 셈이다. 아울러 각각의 퍼셉트론의 출력을 모아서 처리하려면 제3의 퍼셉트론이 필요하게 되며, 웨이트 벡터 W와 바이아스 b가 필요하게 된다.
이 2개의 퍼셉트론 모델을 아예 통합해서 사이즈가 2X2인 웨이트 매트릭스 W를 가지는 1개의 복합된 퍼셉트론으로 모델링하자. 이어서 이 복합된 퍼셉트론으로부터의 출력이 2개이므로 퍼셉트론 하나를 직렬로 추가 연결하여 최종적으로 1개의 값을 출력하도록 NN을 구성하자. 각 파셉트론의 출력에는 반드시 Sigmoid 처리를 하도록 한다. 이와 같이 전형적인 신경망 구성법 외에도 아직 알려지지 않은 다양한 신경망 구성법이 있을 수 있음을 지적해둔다.

이와 같이 NN에서 hypothesis 계산은 least square 기법과는 달리 뉴론에서 처럼 threshold를 넘는 경우에만 firing 하듯이 sigmoid 함수를 도입하여 계산을 수행할 필요가 있다. sigmoid 처리의 역할은 NN의 연산 결과 hypothesis 값이 문턱 값을 넘는 경우에만 출력 값 “1”을 주며 그렇지 않은 경우에는 “0” 으로 처리한다. 여기서는 sigmoid 처리를 하지 않고 최소제곱법을 사용하는 경우 xor_least_square_01.py 의 계산 결과와 sigmoid 처리를 하게 되는 xor_nn_01.py 의 2가지 경우를 각각 비교해 보기로 한다.
TensorFlow 코드 학습을 위한 데이터를 아래와 같이 리스트 데이터 구조를 가지도록 준비하자.
x_data = [[0, 0],[0, 1],[1, 0],[1, 1]], y_data = [[0],[1],[1],[0]]
즉 리스트 데이터인 x_data 가 4개의 [x1, x2] 를 제공한다.
NN에서는 퍼셉트론 처리 결과에 sigmoid 함수를 적용한 파이선 코드 xor_nn_01.py를 실행하도록 하자. 최소제곱법 퍼셉트론 코드 xor_least_square_01.py 와의 차이점은 다음과 같다.

물론 NN에서의 마지막 레이어가 sigmoid 처리이므로 최소제곱법과는 달리 그에 맞춰 cost함수를 구성해 주도록 한다.

그렇지 않으면 hypothesis 값이 분리선 결정이 불가능한 0.5 를 준다는 점에 유의한다. 각자 계산을 통해 확인해 볼 필요가 있을 듯하다.
아나콘다에서 코드를 실행하여 아래와 같이 hypothesis를 비롯한 파라메터들의 값을 관찰하도록 하자. 동일한 steps 수를 사용했음에도 단순 퍼셉트론형 계산은 다음과 같이 실패한 결과를 주지만

반면에 learning rate = 0.1, 반복학습 횟수 10,000 일 때에 Sigmoid 함수를 사용하는 NN 계산법의 경우 표에서 hypothesis 값을 살펴보면 거의 0.0,1.0,1.0,0.0 에 근접함을 알 수 있다.

이 데이타를 사용하여 NN은 다음과 같이 나타낼 수 있다. 더욱 세분화하여 개별 노드와 엣지를 넣어서 표현하면 아래와 같은 뉴럴 네트워크 다이아그램이 얻어진다.

이와 같은 노드 다이아그램은 TensorFlow 코딩에서 Tensor Board 를 사용하여 코드의 상세한 GRAPH 구조를 모니터 할 수 있다.
여기서 layer1 이라는 변수 명을 사용했는데 입력과 출력 사이에 이러한 layer를 필요에 따라 얼마든지 코딩해 넣을 수 있다. 이렇게 임의로 추가할 수 있는 layer들을 은닉 층(hidden layer) 이라고 하며 Deep Learning 의 출발점이 된다.

첨부된 파이선 코드를 실행해 보자. 단 session = tf.Session() 이하 영역에서 indentation 이 무너진 부분을 반드시 복구하여 실행하기 바란다
#xor_nn_01.py
import tensorflow as tf
import numpy as np
tf.set_random_seed(777) # for reproducibility
learning_rate = 0.1
x_data = [[0, 0],
[0, 1],
[1, 0],
[1, 1]]
y_data = [[0],
[1],
[1],
[0]]
x_data = np.array(x_data, dtype=np.float32)
y_data = np.array(y_data, dtype=np.float32)
X = tf.placeholder(tf.float32, [None, 2])
Y = tf.placeholder(tf.float32, [None, 1])
W1 = tf.Variable(tf.random_normal([2, 2]), name='weight1')
b1 = tf.Variable(tf.random_normal([2]), name='bias1')
layer1 = tf.matmul(X, W1) + b1
W2 = tf.Variable(tf.random_normal([2, 1]), name='weight2')
b2 = tf.Variable(tf.random_normal([1]), name='bias2')
hypothesis = tf.matmul(layer1, W2) + b2
#cost/loss function
#cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
#tf.log(1 - hypothesis))
cost = tf.reduce_mean(tf.square(hypothesis - Y))
train = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
#Accuracy computation
#True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))
#Launch graph
with tf.Session() as sess:
#initialize TensorFlow variables
sess.run(tf.global_variables_initializer())
for step in range(10001): sess.run(train, feed_dict={X: x_data, Y: y_data}) if step % 5000 == 0: print(step, sess.run(cost, feed_dict={ X: x_data, Y: y_data}), sess.run([W1, W2]), sess.run([b1, b2])) #Accuracy report h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data}) print("\nHypothesis: ", h, "\nCorrect: ", c, "\nAccuracy: ", a)
'''
Hypothesis: [[ 0.01338218]
[ 0.98166394]
[ 0.98809403]
[ 0.01135799]]
Correct: [[ 0.]
[ 1.]
[ 1.]
[ 0.]]
Accuracy: 1.0
'''
#xor_nn_01.py
#XOR
import tensorflow as tf
import numpy as np
tf.set_random_seed(777) # for reproducibility
learning_rate = 0.1
x_data = [[0, 0],
[0, 1],
[1, 0],
[1, 1]]
y_data = [[0],
[1],
[1],
[0]]
x_data = np.array(x_data, dtype=np.float32)
y_data = np.array(y_data, dtype=np.float32)
X = tf.placeholder(tf.float32, [None, 2])
Y = tf.placeholder(tf.float32, [None, 1])
W1 = tf.Variable(tf.random_normal([2, 2]), name='weight1')
b1 = tf.Variable(tf.random_normal([2]), name='bias1')
layer1 = tf.sigmoid(tf.matmul(X, W1) + b1)
W2 = tf.Variable(tf.random_normal([2, 1]), name='weight2')
b2 = tf.Variable(tf.random_normal([1]), name='bias2')
hypothesis = tf.sigmoid(tf.matmul(layer1, W2) + b2)
#cost/loss function
cost = -tf.reduce_mean(Y * tf.log(hypothesis) + (1 - Y) *
tf.log(1 - hypothesis))
train = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
#Acuuracy computation
#True if hypothesis>0.5 else False
predicted = tf.cast(hypothesis > 0.5, dtype=tf.float32)
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32))
#Launch graph
with tf.Session() as sess:
#initialize TensorFlow variables
sess.run(tf.global_variables_initializer())
for step in range(10001): sess.run(train, feed_dict={X: x_data, Y: y_data}) if step % 5000 == 0: print(step, sess.run(cost, feed_dict={ X: x_data, Y: y_data}), sess.run([W1, W2]), sess.run([b1, b2])) #Accuracy report h, c, a = sess.run([hypothesis, predicted, accuracy], feed_dict={X: x_data, Y: y_data}) print("\nHypothesis: ", h, "\nCorrect: ", c, "\nAccuracy: ", a)
'''
Hypothesis: [[ 0.01338218]
[ 0.98166394]
[ 0.98809403]
[ 0.01135799]]
Correct: [[ 0.]
[ 1.]
[ 1.]
[ 0.]]
Accuracy: 1.0
'''
'머신러닝' 카테고리의 다른 글
| 3-7 집합계산 방식의 softmax XOR 논리 처리 (0) | 2021.07.02 |
|---|---|
| 3-6 NN(Neural Network)이 아닌 집합계산 원리를 이용한 Perceptron XOR 논리 처리 (0) | 2021.07.02 |
| 3-4 XOR 로직 머신 러닝: 성냥개비 하나로 (0,1) 과 (1,0) 점을 (0,0)과 (1,1) 점을 분리하라! (0) | 2021.07.02 |
| 3-1 OR 로직 머신 러닝 (0) | 2021.07.02 |
| 2-17 Iris flower data를 이용한 Rosenblatt 퍼셉트론 파이선 코딩 (0) | 2021.07.02 |