갈릴레오의 실험

피사의 탑에서 가벼운 구슬과 무거운 구슬을 떨어뜨릴 때 당연히 무거운게 빨리 떨어지고 가벼운 것이 천천히 떨어질것이라는 아이디어는 갈릴에오에 의해 두 구슬이 같이 떨어진다는 실험 결과로 결론이 맺어졌다.
하지만 자세히 보면 구슬에 중력 뿐만 아니라 공기 저항에 의한 항력도 작용함을 알 수 있다.
갈릴레오 이후 발전된 유체역학에 의하면 볼 표면을 따라서 경계층류 (Boundar Layer Flow)가 발달하여 항력을 미친다는 사실이 알려졌다.
자유낙하

항공기에 작용하는 힘들을 본격적으로 다루어 보기 전에 질점에 작용하는 중력과 항력을 다루는 간단한 문제로부터 시작하자.
갈릴레오의 피사 사탑에서 행한 낙하실험은 중력의 영향만을 고려하였다. 이를 뉴턴의 법칙에 따라 풀어 보기로 한다.
옆 그림을 분석해 보면 질량 m에 작용하는 모든 외력들은 중력에 의한 무게(W=-mg)밖에 없으며 물체가 받게 되는 힘은 즉 질량×가속도이므로 뉴튼의 2법칙으로 부터 y에 관한 2계 상미분 방전식 형태로 운동방정식이 얻어진다.
중력가속도 g=9.8 m/s2 이며, 질량 m을 낙하시키는 초기 위치 y(0)=10 m, 초기 속도 v(0)=0 m/s로 둔다.
운동 방정식을 풀기 위해 2회 연속으로 적분하였을 때 얻어지는 일반해는 아래와 같이 주어진다.

단, 수식 표현에 들어 있는 C1과 C2는 적분 상수로서 부정적분 1회 실시 후 적분 상수를 C1으로, 부정적분 2회차 실시 후 적분상수를 C2로 둔다.
학습) 운동 방정식을 세워 얻어지는 2계 상미분 방정식을 주어진 초기 조건들을 사용하여 풀어 보자.
y(t)=0 조건을 사용하여 질량 m이 지면에 닿을 때까지 소요 시간과 속도를 계산해 보자.
중력가속도 g=9.8 m/s2 이고, 계산 결과는 소수점 둘째자리에서 반올림 처리한다.
풀이) t=(20/g)0.5=(20/9.8)0.5=1.43s
v=g∙t=(9.8)×(1.43)=14.0m/s
공기 유체의 지배운동 방정식과 레이놀즈 수
공기중에서 낙하하는 볼의 운동과 같이 간단한 문제를 다루기 위해서도 해를 얻기 위해서는 Navier Stokes 방정식을 풀어야 할것이다. 하지만 비선형성으로 인해 이 방정식을 풀어내기란 쉽지 않다. 아래는 비압축성 조건하에서의 방정식 형태이다. 항공역학에서 공기의 압축성 효과가 나타나기 시작하는 경계는 근사적으로 마하 수 M = 0.3 이상으로 본다. 별도의 외력의 영향이 없는 경우를 고려해 보자.

이 방정식으로 항공기 날개 주위의 유동을 고려할 경우 날개의 시위(chord) 길이가 L, 항공기 비행 속도가 U0 라면 상기 방적식의 각 항들은 다음과 같이 근사적으로 평가할 수 있다.


이로부터 점성마찰항에 대한 관성항의 비율에 해당하는 무차원 레이놀즈 수 Re를 다음과 같이 평가할 수 있다.
Navier Stokes 방정식을 풀기는 거의 불가능하지만 풍동실험이나 실제 비행을 통해 항공기 날개의 양력이나 항력 값을 알아낼 수 있으므로 레이놀즈 수 Re 수는 편리한 기준이 될 수 있다.
항공기 이륙전의 정지상태라면 Re 값이 거의 0 이라 볼 수 있으며 9km(30,000 feet) 상공에서 거의 마하 수 1 가까이 천음속 비행 시는 Re 수 대단히 큰 값을 가지게 된다. 하지만 날개 아주 가까이에서는 여전히 무시할 수 없을 정도의 boundary layer 에 의한 점성 마찰이 존재한다.
구형 물체 주위의 공기흐름

항공기처럼 공기 중에서 운동하는 물체의 동력학 해석을 위해서는 물체에 가해지는 힘으로서 공기와 물체 사이의 마찰에 기인한 항력을 반드시 고려해야 한다. 구형 물체는 수직 운동 방향에 대해 대칭이므로 수평 방향으로 작용하는 힘 예를 들자면 양력은 없을 수 밖에 없으며 항력만이 작용하여 낙하 운동을 지연시키게 될 것이다. 갈릴레오의 낙하실험에 사용된 것처럼 일정한 크기의 직경과 형상을 가지는 공(sphere) 모양의 볼에 대해서 아래의 항력 실험 그래프를 사용하여 항력계수 Cd를 결정하는 방법을 알아보자. 이런 유형의 항력을 form drag 이라한다.(참조: http://blog.daum.net/ejleep1/1309) 즉 물체가 유체속을 뚫고 운동하게 되면 이를 저지하기 위해 형성되는 압력 프로파일에 의한 항력이다.
아래의 log-log 챠트에서, 레이놀즈 수 100 ~100000 사이는 거의 비슷한 Cd 값임을 알 수 있다.

볼의 직경이 2.0cm, 속력이 8m/s, 공기의 점도가 1.456×10의 -5승 m2/s 일 때, 항력계수 즉 Cd를 결정하기 위해서, 무차원 레이놀즈수(Re=Vd/ν)를 계산하여 항력계수 Cd의 값을 그래프에서 읽어보자. 이때 계산된 레이놀즈수와 항력계수 Cd의 값은 얼마인지 계산해보자.
참고: McComick의 Aerodynamics, Aeronautics and Flight Mechanics, .... 177 페이지 연습문제에서 실린더 대신 구형으로 문제를 바꾸었다.
계산결과 Re = 1.099x10의 4승이며 위 그래프에서 Smooth sphere 곡선의 값을 읽으면 Cd = 0.47 가 된다.
설사 볼의 크기와 점도가 일정하다는 조건하에서 낙하속도가 10배정도 커진다고 해도 레이놀즈 수가 10만 정도이므로 Cd 값이 거의 일정하기때문에 Galileo 의 실험은 레이놀즈 수가 상당히 변화하드라도 공기 항력의 영향을 그다지 받지 않을 것이다는 점을 알 수 있다. Galileo 의 낙하실험에서는 여러번 되풀이해도 일치하는 결과를 얻을 수 있었을 것이다. 이러한 면에서 Galileo는 운이 좋았다고 볼 수 있을 것이다.

항력 계수가 결정되면 항력은 다음 공식을 사용하여 계산할 수 있다.
이 공식에서 ρ는 공기의 밀도를, A는 물체의 단면적을 나타낸다. 이와 같이 얻어낸 항력을 감안하면서 옆 그림의 자유물체도를 참고하면서 중력의 영향으로 낙하하는 볼에 대해서 뉴튼의 2법칙에 따라 운동 방정식을 수립해보자.
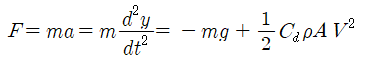
이 방정식을 자세히 살펴보면 항력 항에 속도 제곱항이 있음을 알수 있다. 즉 V=dy/dt 항이 포함됨으로 인해 결국 이 문제는 비선형 상미분 방정식 문제로 귀착됨을 알 수 있다. 물선 비선형이긴

하지만 풀이가 가능하다. 이러한 미분 방정식은 미국판 Bedford & Fowlwr의 동력학 교과서인 Dynamics/Engineering Mechanics 34페이지 항공기의 파라슈트에 의한 감속 문제에서 공기역학적인 배경 설명 없이 이용되고 있다.

이 문제 자체를 직접 수치계산할 필요는 없으며 운동 방정식 수립이 가능하다면 파라슈트 감속문제를 직접 풀어 보도록 하자. 파라슈트 감속은 활주로 길이가 짧은 항공기 착륙 시에 일어날 수 있는 기급상황으로 볼 수 있으며 특히 우주왕복선의 착륙 시 시속이 500 km/h 가 넘을 정도로 속도가 높기때문에 파라슈트 감속이 필수적이 된다.
이미 지상에서 활주 중인 우주왕복선의 주행 방향 중력 영향은 없다고 가정하면, 앞서의 운동방정식은 다음과 같이 간략화 된다. 단 이 미분 방정식에서 현재 고려하는 항공기의 질량, 공기 밀도, 항공기의 항력 수, 단면적을 감안하여 상수 c의 값을 0.004로 설정하고 파라슈트가 감속 효과를 내기 시작하는 시점의 속도를 시속 500 km/h 에 해당하는 v0 = 140 m/s 로 설정하자.
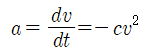
이 방정식은 공업수학의 변수변리 기법으로 간단히 풀 수 있다. 항공기 진행 방향으로 좌표축을 s로 두고 변수 분리 후 적분하도록 한다. 이러한 접근법의 문제점은 v=0에서 값이 발산하므로 v>0 인 범위까지만 계산이 가능하다.
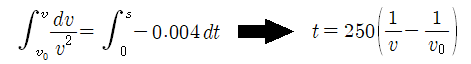
학습문제)이 공식을 사용하여 항공기 속도 v0= 140 m/s 에서 v = 10 m/s 까지 감속될때까지 몇 초가 걸리는지 계산해 보아라.
v=0에서 계산이 실패하는 이유는 명확하다. 레이놀즈 수 범위가 100 ~100000 사이를 벗어나 0에 거의 가까워지기때문에 항력계수 모델이 더 이상 다당하지 않는 영역으로 들어가기 때문이다. 특히 레이놀즈 수가 10 이하일 경우에는 관성항의 효과를 무시할 수 있기때문에 Navier Stokes 방정식이 선형화 될 수 있는데 이 방정식을 Stokes 방정식이라고 한다. 레이놀즈 수가 아주 작은 경우엔점성항과 압력 그라디엔트 항에 의해 흐름이 일어나며 특히 공기가 아닌 비압축성 액체인 경우 바이오 과학 분야에서 혈관내 혈소판의 운동과 같은 마이크로한 유체흐름을 다루는데 편리하다고 한다.
하지만 현재의 중요 관심사가 항공기이므로 다루어야 할 레이놀즈 수 법위가 상당히 높은 영역에서 평판 또는 얇은 에어포일 주위의 공기 흐름에 더욱 관심을 가져 보기로 하자.
항공모함과 같이 착륙을 위한 활주길이가 대단히 짧은 경우 착륙과 거의 동시에 항공기 후미의 훜을 사용하여 탄력적으로 항공기를 낚아채어 활주길이를 줄이는 사례도 참조하자.

Under Construction...
'항공기 공기역학' 카테고리의 다른 글
| 항공기에 작용하는 항력, 양항비 (0) | 2022.06.04 |
|---|